# GraphSAGE:我寻思GCN也没我牛逼(NIPS-2017)

众所周知,2017年ICLR出产的GCN现在是多么地热门,仿佛自己就是图神经网络的名片。然而,在GCN的风头中,很多人忽略了GCN本身的巨大局限——Transductive Learning——没法快速表示新节点,这限制了它在生产环境中应用。同年NIPS来了一篇使用Inductive Learning的GraphSAGE,解决了这个问题。今天,让我们来一起琢磨琢磨这个GraphSAGE是个什么玩意儿。
# 一、回顾GCN及其问题
GCN的基本思想: 把一个节点在图中的高纬度邻接信息降维到一个低维的向量表示。
GCN的优点: 可以捕捉graph的全局信息,从而很好地表示node的特征。
GCN的缺点: Transductive learning的方式,需要把所有节点都参与训练才能得到node embedding,无法快速得到新node的embedding。
得到新节点的表示的难处:
要想得到新节点的表示,需要让新的graph或者subgraph去和已经优化好的node embedding去“对齐”。然而每个节点的表示都是受到其他节点的影响,因此添加一个节点,意味着许许多多与之相关的节点的表示都应该调整。这会带来极大的计算开销,即使增加几个节点,也要完全重新训练所有的节点,这可太费劲了。
因此我们需要换一种思路:
既然新增的节点,一定会改变原有节点的表示,那么我们干嘛一定要得到每个节点的一个固定的表示呢?我们何不直接学习一种节点的表示方法。这样不管graph怎么改变,都可以很容易地得到新的表示。
# 二、GraphSAGE是怎么做的
针对这种问题,GraphSAGE模型提出了一种算法框架,可以很方便地得到新node的表示。
基本思想:
去学习一个节点的信息是怎么通过其邻居节点的特征聚合而来的。 学习到了这样的“聚合函数”,而我们本身就已知各个节点的特征和邻居关系,我们就可以很方便地得到一个新节点的表示了。
GCN等transductive的方法,学到的是每个节点的一个唯一确定的embedding; 而GraphSAGE方法学到的node embedding,是根据node的邻居关系的变化而变化的,也就是说,即使是旧的node,如果建立了一些新的link,那么其对应的embedding也会变化,而且也很方便地学到。
GraphSAGE具体从三部分讲解:
# 1. Embedding generation
即GraphSAGE的前向传播算法。

上面的算法的意思是:
假设我们要聚合K次,则需要有K个聚合函数(aggregator),可以认为是N层。 每一次聚合,都是把上一层得到的各个node的特征聚合一次,在假设该node自己在上一层的特征,得到该层的特征。如此反复聚合K次,得到该node最后的特征。 最下面一层的node特征就是输入的node features。
用作者的图来表示就是这样的:(虽然酷炫,但有点迷糊)
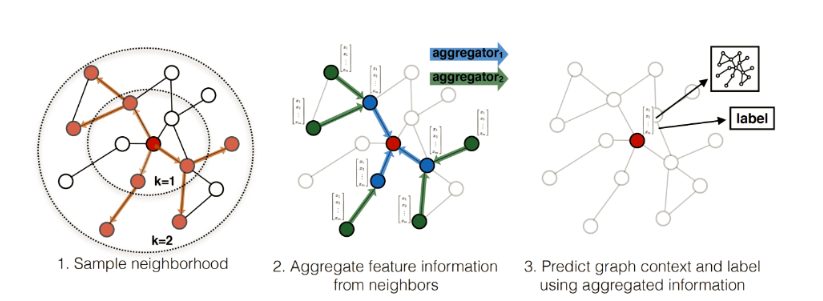
我来画一个图说明:(虽然朴素,但是明明白白)
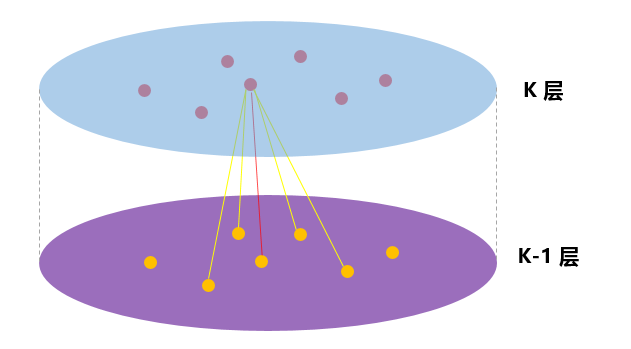
这里需要注意的是,每一层的node的表示都是由上一层生成的,跟本层的其他节点无关。
# 2. GraphSAGE的参数学习
在上面的过程中,我们需要学习各个聚合函数的参数,因此需要设计一个损失函数。 损失函数是设计是根据目标任务来的,可以是无监督的,也可以是有监督的。
对于无监督学习,我们设计的损失函数应该让临近的节点的拥有相似的表示,反之应该表示大不相同。所以损失函数是这样的:
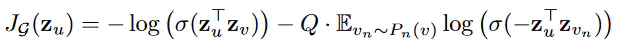
也没什么好解释的。 对于有监督学习,可以直接使用cross-entropy。
# 3. 聚合函数的选择
这里作者提供了三种方式:
Mean aggregator :
直接取邻居节点的平均,公式过于直白故不展示。GCN aggregator: 这个跟mean aggregator十分类似,但有细微的不同,公式如下:
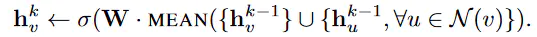 把这个公式,去替换前面给的Algorithm1中的第4,5行。
自己体会一下哪里不同。想不明白的留言。实际上,这个几乎就是GCN中的聚合方式,想一想为啥。
把这个公式,去替换前面给的Algorithm1中的第4,5行。
自己体会一下哪里不同。想不明白的留言。实际上,这个几乎就是GCN中的聚合方式,想一想为啥。LSTM aggregator:
使用LSTM来encode邻居的特征。 这里忽略掉邻居之间的顺序,即随机打乱,输入到LSTM中。这里突然冒出来一个LSTM我也是蛮惊讶,作者的想法是LSTM的表示能力比较强。但是这里既然都没有序列信息,那我不知道LSTM的优势在何处。Pooling aggregator:
把各个邻居节点单独经过一个MLP得到一个向量,最后把所有邻居的向量做一个element-wise的max-pooling或者什么其他的pooling。公式如下:
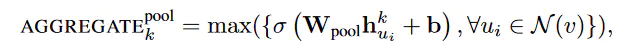
这就是GraphSAGE的主要内容了,其实思路还是十分简洁的,理解起来也比GCN容易多了。
# 邻居的定义:
前面一直都没讨论一个点,那就是如何选择一个节点的邻居以及多远的邻居。
这里作者的做法是设置一个定值,每次选择邻居的时候就是**从周围的直接邻居(一阶邻居)**中均匀地采样固定个数个邻居。
那我就有一个疑问了?每次都只是从其一阶邻居聚合信息,为何作者说:
随着迭代,可以聚合越来越远距离的信息呢?
后来我想了想,发现确实是这样的。虽然在聚合时仅仅聚合了一个节点邻居的信息,但该节点的邻居,也聚合了其邻居的信息,这样,在下一次聚合时,该节点就会接收到其邻居的邻居的信息,也就是聚合到了二阶邻居的信息了。
还是拿出我的看家本领——用图说话:
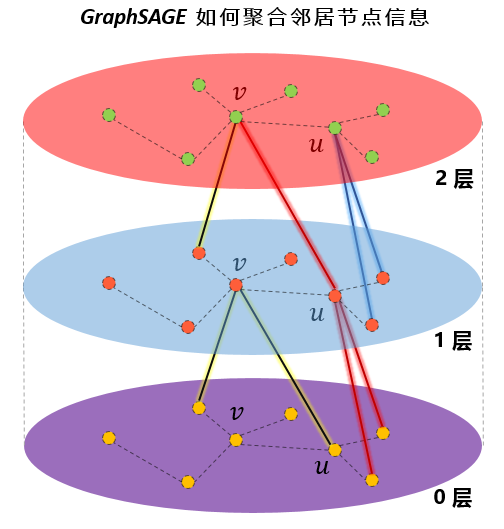
我的天,这个图简直画的太好了吧。
图中(为了图的简洁,这里假设只随机聚合两个邻居)可以看出,层与层之间,确实都是一阶邻居的信息在聚合。在图中的“1层”,节点v聚合了“0层”的两个邻居的信息,v的邻居u也是聚合了“0层”的两个邻居的信息。到了“2层”,可以看到节点v通过“1层”的节点u,扩展到了“0层”的二阶邻居节点。因此,在聚合时,聚合K次,就可以扩展到K阶邻居。
在GraphSAGE的实践中,作者发现,K不必取很大的值,当K=2时,效果就灰常好了,也就是只用扩展到2阶邻居即可。至于邻居的个数,文中提到S1×S2<=500,即两次扩展的邻居数之际小于500,大约每次只需要扩展20来个邻居即可。这也是合情合理,例如在现实生活中,对你影响最大就是亲朋好友,这些属于一阶邻居,然后可能你偶尔从他们口中听说一些他们的同事、朋友的一些故事,这些会对你产生一定的影响,这些人就属于二阶邻居。但是到了三阶,可能基本对你不会产生什么影响了,例如你听你同学说他同学听说她同学的什么事迹,是不是很绕口,绕口就对了,因为你基本不会听到这样的故事,你所接触到的、听到的、看到的,基本都在“二阶”的范围之内。
# 三、效果与性能分析:
这个部分是最没意思的,毕竟谁发paper不是说自己的模型最牛逼?
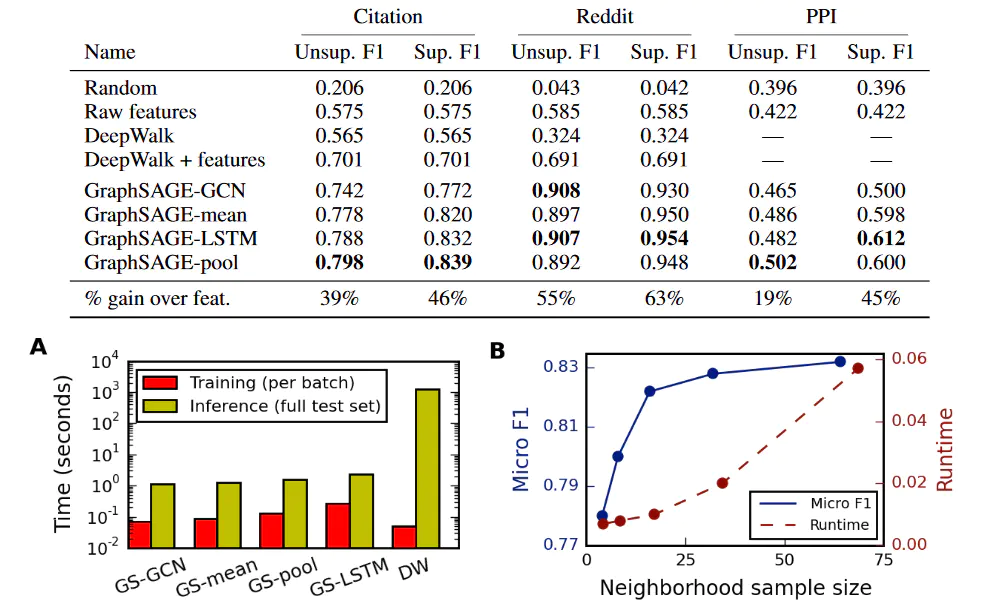
这个部分我不想多说,三个图都很好理解。
# (彩蛋)思考 & GCN的反刍:
在看完GraphSAGE之后,我又回头把GCN思考了一遍。从直观上去看,我一开始觉得GraphSAGE和GCN截然不同,后来发现只是论文作者的介绍的角度不同,实际上两者的本质上没有很大差别。或者说,懂了GraphSAGE的原理之后,再去看GCN,会发GCN没那么难以理解了。
来人啊,GCN公式搬上来:
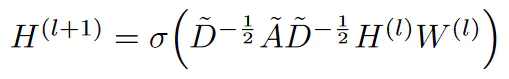
额,,,这个是丑版本的公式,还是上美版本的吧:
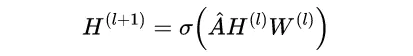
中间这个A帽子,就是上面丑公式中的那一大串东西。对A帽子的理解,其实它就是邻接矩阵A做的一个归一化。下面为了表达的方便,我直接当做邻接矩阵来分析吧!H是节点的每一层的特征矩阵。
这个公式的内部,画成矩阵相乘的形式是这样的:
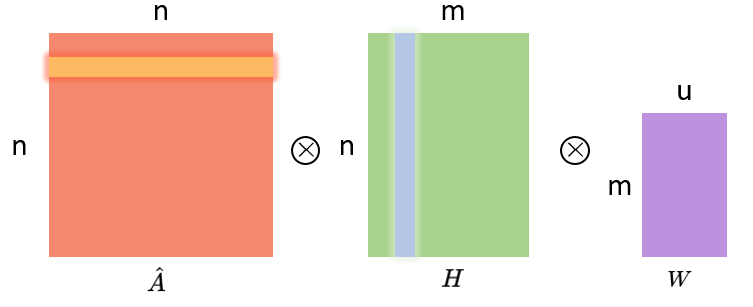
其中,A是n×n维,H是n×m维,W则是m×u维。n就是节点个数,m则是节点特征的维度,u就是神经网络层的单元数。
我们先看看A乘以H是个啥意思:
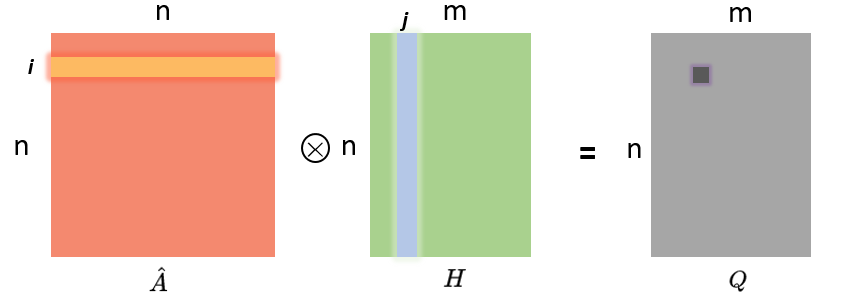
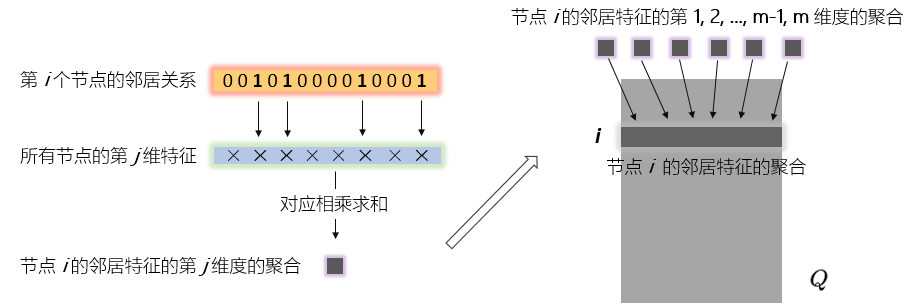
A帽子矩阵的第i行和H矩阵的第j列对应元素相乘在求和就得到Q矩阵的(i,j)个元素。 这都是最基本的线性代数了,但我们不妨再仔细看看我图中高亮的那几个向量的内部:
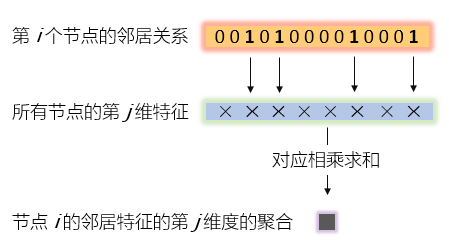
这个图说的明明白白,所以我们发现,GCN的这一步,跟GraphSAGE是一样的思想,都是把邻居的特征做一个聚合(aggregation)。
所以,都是一个词——Aggregate!Aggregate就完事儿了。
这也是为什么GraphSAGE的作者说,他们的mean-aggregator跟GCN十分类似。在GCN中,是直接把邻居的特征进行求和,而实际不是A跟H相乘,而是A帽子,A帽子是归一化的A,所以实际上我画的图中的邻居关系向量不应该是0,1构成的序列,而是归一化之后的结果,所以跟H的向量相乘之后,相当于是“求平均”。GraphSAGE进一步拓展了“聚合”的方法,提出了LSTM、Pooling等聚合方式,不是简单地求平均,而是更加复杂的组合方式,所以有一些效果的提升也是在情理之内的。
至于说为什么GCN是transductive,为啥要把所有节点放在一起训练? 我感觉不一定要把所有节点放在一起训练,一个个节点放进去训练也是可以的。无非是你如果想得到所有节点的embedding,那么GCN可以让你一口气把整个graph丢进去,直接得到embedding,还可以直接进行节点分类、边的预测等任务。
其实,通过GraphSAGE得到的节点的embedding,在增加了新的节点之后,旧的节点也需要更新,这个是无法避免的,因为,新增加点意味着环境变了,那之前的节点的表示自然也应该有所调整。只不过,对于老节点,可能新增一个节点对其影响微乎其微,所以可以暂且使用原来的embedding,但如果新增了很多,极大地改变的原有的graph结构,那么就只能全部更新一次了。从这个角度去想的话,似乎GraphSAGE也不是什么“神仙”方法,只不过生成新节点embedding的过程,实施起来相比于GCN更加灵活方便了。我们学习到了各种的聚合函数之后,其实就不用去计算所有节点的embedding,而是我们需要去考察哪些节点,就现场去计算,这种方法的迁移能力也很强,在一个graph上学得了节点的聚合方法,到另一个新的类似的graph上就可以直接使用了。
好啦,关于GraphSAGE的介绍就到这里,我个人在读了这篇文章后还是收获颇丰的,尤其是和GCN对比的过程,让我对二者都有了更加深刻的认识。
