# 样本混进了噪声怎么办?通过Loss分布把它们揪出来!
前言:今天继续分享一篇很有意思的文章,来自2019年ICML的“Unsupervised Label Noise Modeling and Loss Correction”,本文发现了一个“大家都知道但又不太确定”的现象——noisy样本的loss一般比较大,通过实验证实了这一点,并利用这个特点来定位noise从而排除这些noise的影响,来提高模型的性能。可以说是挺有趣了!

- 论文标题:Unsupervised Label Noise Modeling and Loss Correction
- 会议/期刊:ICML-19
- 团队:Dublin City University (DCU)
# 一、本文的主要思想、贡献
- 首先发现并证实了,神经网络在学习“随机的标签”或“错误的标签”(都可以称为噪音样本)的时候,会比学习“正确的标签”要慢,由此发现噪音样本在训练时的loss更大;
- 通过对样本的loss distribution进行观察,作者发现可以使用一个Beta分布来刻画正常样本和噪音样本,从而将二者区分;
- 由此,作者设计了一种复合的模型,在训练的期间,可以通过一种无监督的方式来实时辨别噪声并去除,从而提高模型效果。
下面稍微详细地介绍一下:
# 二、关于Training with noise的一些研究背景
当训练样本中混有噪音,就很容易让模型过拟合,学习到错误的信息,因此必须加以干涉,来控制噪音带来的影响。这方面的研究,主要集中于“损失修正”方法,即loss correction。典型的方法有这些:
# 1. Bootstrapping loss(☆)
这是我非常喜欢的一个loss function,十分的简洁,又有道理,让人一见钟情。公式如下:
上面的公式,实际上是指"hard bootstrapping loss"。这里的yi就是真实的标签(一般是one-hot形式的),zi则是预测的标签(也是转化成one-hot形式的,因此叫hard),然后hi就是预测的概率分布。
这个loss实际上就是对cross-entropy loss的一个修正,把真实标签改了改,分了一部分到预测出来的那个维度上。
这样做的效果是什么?首先我们得有一个概念:
如果一个样本的损失很小,模型就不会在这个样本上面花太多功夫去拟合它;相反,损失很大,模型就会花大力气去拟合它。
那么,对一个噪音点,其相比于正常点,计算出来的loss一般都会更大一些(label跟实际的相差较远),因此模型会花大力气去拟合这些噪音点,因此传统的cross-entropy loss是鼓励模型学习到错误信息的。而bootstrapping loss,把模型自己的预测,加入到真实标签中,这样就会直接降低这些噪音点的loss(极端一点,如果真实标签就是模型的预测,那loss就趋于0),因此模型会降低对噪音点的注意力;对于正常的样本,zi带来的影响相对会较小(zi更容易跟yi一致),因此正常样本还是可以得到有效的训练。
是不是真·有、意思?
这个B-loss来自2015ICLR,目前引用量高达467次了。。。好东西大家都喜欢啊。
# 2. Curriculum learning
Curriculum learning这名字一听就很有意思,“课程学习”往往是由浅入深、先易后难的,这个curriculum learning也是这个思想,最早由Bengio在09年的时候提出,思想就是:
“把训练样本按照一个有意义的顺序(比如先易后难)排列,有助于加快模型的迭代和泛化性能。”
因此有学者使用这样的思想,把clean样本视为简单的,noisy样本视为困难的,来让模型学习。具体的方法还是通过改变clean和noisy样本的loss权重来实现这个目的。
# 3. Mixed data augmentation
这个方法也比较有新意,通过一种数据增强的方法,来减少noise带来的影响:
具体则是将clean和noisy的样本和标签进行结合,得到新样本和新标签。
简单的理解为将两个不同的样本做了一个平均,平均肯定更加稳定嘛!
# 4.其他:
其他的我就没细看了,比如使用一个noise transition matrix来调整loss或者预测概率等等。
# 三、本文提出的方法:
本文提出的方法思路也十分清晰:
- 第一步:通过cross-entropy得到的loss分布来判断样本是noisy还是clean的概率
- 第二步:使用这个概率来动态地调整loss function,使用该loss来训练
# 第一步:Label noise modeling
作者通过实验发现noise和clean在loss上的分布是十分不同的,下图是作者的一个实验结果图:
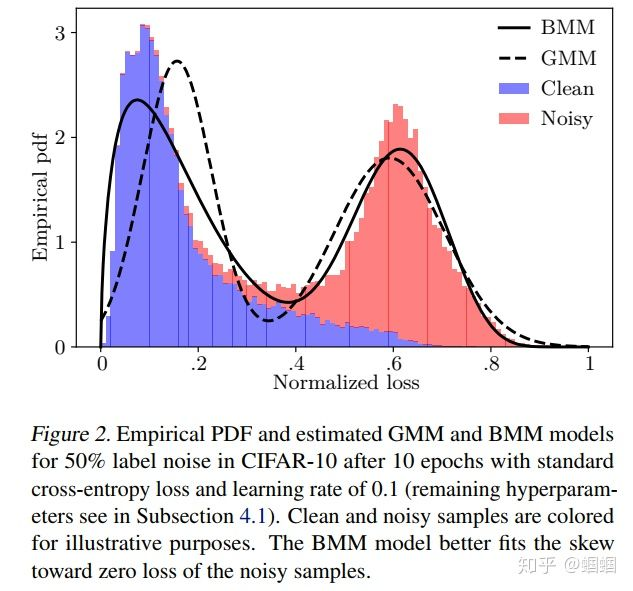
图中展示的是训练了10轮之后的各个样本的cross-entropy loss,可以看出clean和noisy(注意这里是作者为了展示二者的不同而特意标的,实际训练时我们不知道谁是clean谁是noisy)的loss分布呈现出一个双峰分布,这样的分布可以使用混合概率模型来模拟,比如高斯混合模型(GMM),但实际上作者发现用贝塔混合模型(BMM)模拟更好(因为形状更像)。
通过EM算法,可以迭代求解出这个BMM分布的参数,从而根据loss的值计算出属于clean还是noisy的概率。
# 第二步:Noise model for label correction
能够判别一个样本是clean还是noisy,就可以去改进前面提到一些方法了,比如Boostrapping loss方法。
前面提到B-loss的主要思想,就是针对对noise样本来对loss进行修正。但是B-loss中的工事中的权重wi是一个超参数,也就是在训练的时候是固定的,这使得clean样本总是会受到一些不好的影响(wi越大,影响越大),而noisy样本往往又调整的不够(wi越小,效果越少),因此这个就十分不灵活了。
现在,我们知道了一个样本是clean还是noisy的概率,那么就有机会动态地调整wi了,即,吧原来的B-loss,改成:
是不是很简洁?总的来说,本文提出的训练方式就是
还是在原来的使用CE-loss的训练模式下,每个epoch训练完之后,去使用EM算法把当前这个混合贝塔分布BMM给模拟出来,然后计算新的loss——D-loss,使用这个D-loss来更新参数。注意每一轮都是使用CE-loss来学习BMM,然后使用D-loss更新。
其实论文中还提到了一个更加复杂的方法,就是对前面提到的mixup data augmentation的改进,但我感觉普适性不够强,所以这里不再介绍了。
通过作者改造后的loss function,我们可以跟原来的CE-loss做一个对比:
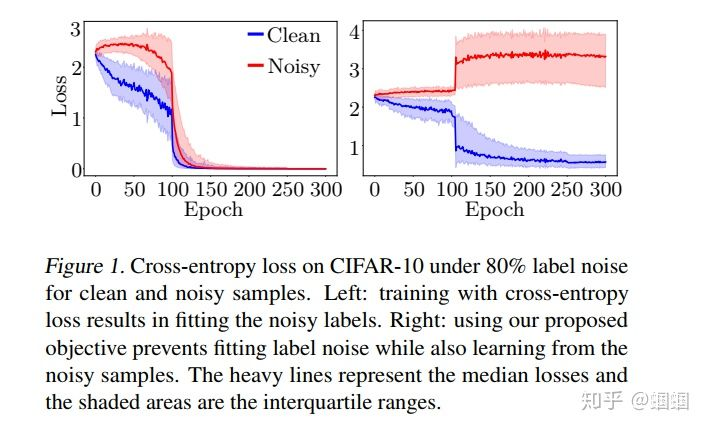
发现,确实可以吧clean和noisy进行很好的区分。
实验的部分,没什么特别的,这里也不多嘴了。
好了,本篇论文解读就到这里了,最让人影响深刻的,应该就是这个Boostrapping Loss和使用BMM来模拟clean/noisy的loss分布的想法了。
