# 标签增强技术(Label Enhancement)
前言:我们习惯于使用one-hot标签来进行模型的训练,但是有没有办法可以构造出更好的标签呢?本文主要根据东南大学的论文“Label Enhancement for Label Distribution Learning”进行解读和整理,从而认识并理解在分类问题中“标签增强”技术。

- 论文标题:Label Enhancement for Label Distribution Learning
- 会议/期刊:IJCAI-18
- 团队:东南大学 计算机科学与工程学院
# 标签分布 & 标签分布学习
标签分布学习(Label Distribution Learning,LDL)的任务是让模型去学习一个样本的标签分布(Label Distribution),即每一个维度都反映对应标签程度的一种概率分布。这样的标签概率分布可以比one-hot更好地表示一个样本的情况,原因主要有以下:
- 一个标签跟样本是否有关,是一个相对的概念,即没有一个“判断是否相关”的绝对标准;
- 当多个标签都跟样本相关时,它们的相关程度一般也是不同的;
- 多个跟样本不相关的标签,它们的不相关程度也一般是不同的。
论文作者给出了几个生动的例子:

然而,LDL任务的主要困难之一就是,标签分布是十分难以获取的。大多数的分类数据集都不具备这样的条件,都只有一些ligical label。所谓logical label,就是指one-hot或者multi-one-hot的label。要获取真实的标签分布,理论上是需要对同一样本进行大量的打标,得到其统计分布的,但这背后的人工成本是无法承受的。
# 主要思想
一个自然的解决办法就是,既然无法从外部得到样本的标签分布,那就使用样本集自身的特征空间来构造出这样的标签分布。

本文把这一类的方法称为label Enhancement(LE),并介绍了几种LE的方法,下面分别作简单的介绍。
# 几种经典的LE方法
# 1. Fuzzy C-Means(FCM)
Fuzzy C-Means 是一个代表性的“软聚类”算法(soft clustering)。它实际上是对K-Means这种“硬聚类”算法的一种改进。K-means聚类只能将一个点划分到一个簇里,而FCM则可以给出一个点归属于各个簇的概率分布。
FCM的目标函数为:
其中是样本点的特征向量,是簇中心的特征向量,是每个点归属于每个簇的系数,类别数,是样本总数。 的计算公式如下,显然离某个簇越近,其系数就越大:
而簇中心的计算方法为,就是所有样本点特征的一个加权平均,其中m是超参数,控制fuzzy的程度,越大簇之间就越模糊:
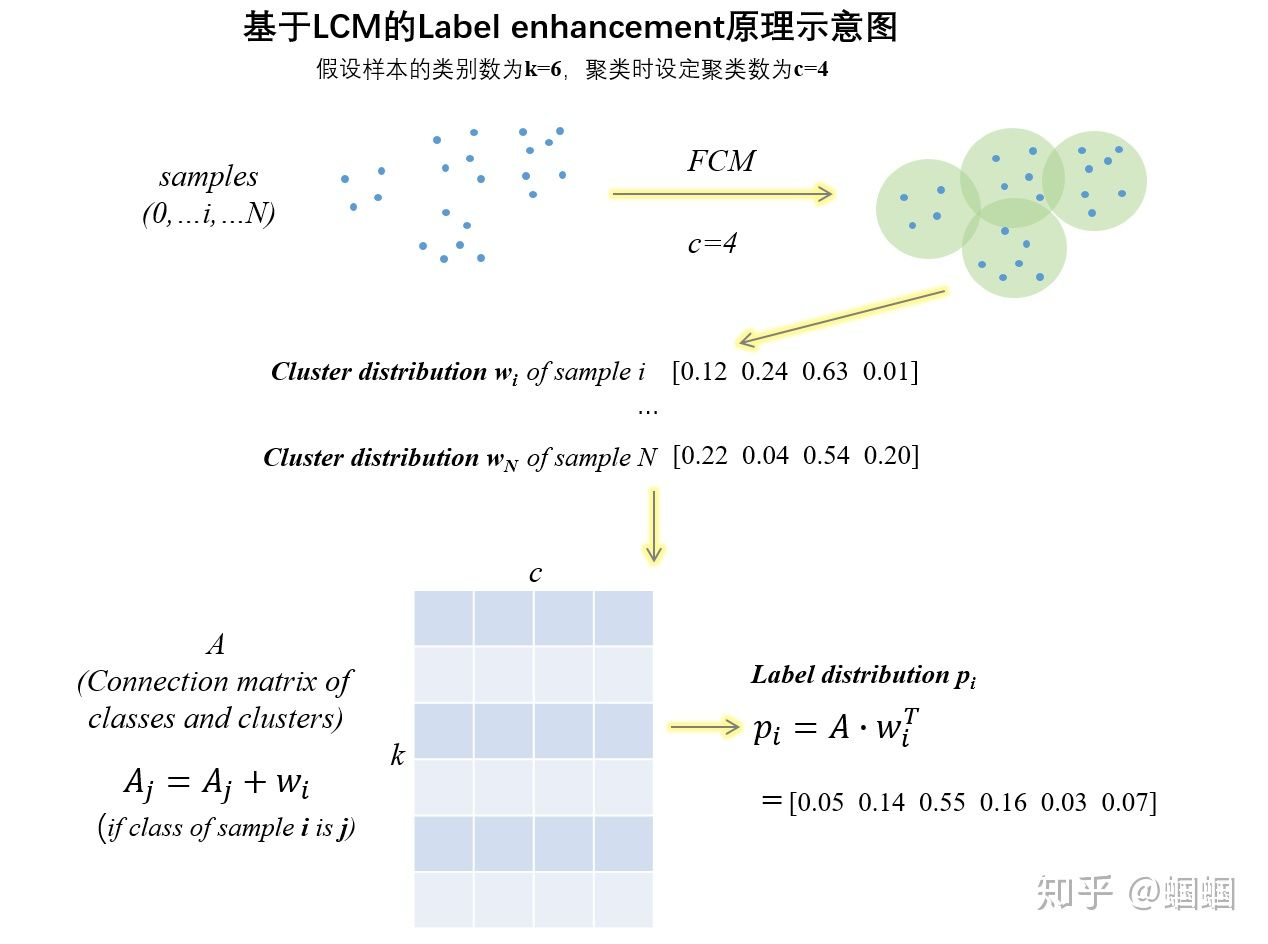
通过FCM算法,如果设置k个簇,样本的簇概率分布就是这个c维向量。
然后,构造一个分类类别(classes)与聚类簇(clusters)之间的一个软连接矩阵k×c的矩阵A:
即A的第j行(代表第j个类别),是由所有属于该类别的样本的簇分布累加而得到的。
最后,通过矩阵A与点乘,就可以将每个样本的簇分布(c个簇),转化为标签分布(k个标签)了。
上面的过程,可以通过下图来表达:
# 2.Label Propagation(LP)
LP的主要思想是通过样本之间的相似度矩阵,来逐步调整原本的logical label representation。
第一步,通过下面的公式,计算N个样本之间的一个N×N的相似性矩阵A:
然后,根据下面的公式,构建label propagation matrix,即标签传导矩阵P:
看到这个公式,熟悉GCN的人会发现,这不就是拉普拉斯矩阵嘛,目的主要是为了让原本的A矩阵归一化和对称。图神经网络的核心,也是邻居节点之间的互相传播,跟这里的相似样本之间,进行标签信息的传播是类似的思想。
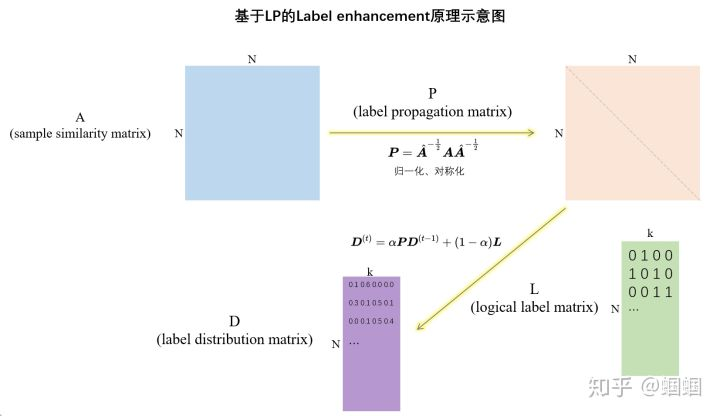
有了这个P传播矩阵,就可以来通过“传播”来构造标签分布D了:
其中L是原本的one-hot的logical label矩阵,D使用L来初始化。
通过不断迭代上式,就可以得到一个趋于稳定的标签分布矩阵D了。
还是照例画一个图:
# 3.Mainifold Learning(LM)
除了LP之外,还有一个Mainifold Learning(LM),主要思想就是假设一个样本点的特征,可以完全由其相邻点的特征线性表示。所谓相邻点,就是通过KNN得到的最近邻。 所以第一步就是优化下面的目标:
学习出相似节点之间的互相表示的方法,即某个点是如何被其他的邻近点所线性表示的。
然后,再去优化这个目标,得到标签分布:
以上是三种传统的Label Enhancement方法。虽然传统,但是其思想我觉得我觉得都挺有意思的,由其是FCM和LP方法。
# 本文提出的新方法:GLLE
GLLE全称为Graph Laplacian Label Enhancement。也是一种基于图的思想的方法。
别看这个名字这么复杂,其实其思想很简单:
在训练标签预测模型的同时,也考虑学习标签间的相似性。
假设我们的预测模型是这样的:
这里的d,就是要学习的标签分布,W就是这个预测模型的参数。
根据前面提到的思想,作者设计的目标函数是这样的,由两部分组成:
前一个部分,就是一个普通的MSE损失函数或最小二乘损失:
如果只优化这个目标,那么得到的就是一个倾向于one-hot/logical label的预测模型。
第二部分,希望相似的样本其分布也相似:
其中这里的a是表达样本i和j之间的相似系数,公式如下:
可以发现,这里计算相似性的方法,跟Label Propagation十分相似,只是多了一个“仅在最近邻范围内计算相似度”这样的限制,因此作者称之为“local similarity matrix”。
后面作者当然扯了一大堆这个目标怎么求解这个优化问题巴拉巴拉,我是不太懂的,感觉是可以使用梯度下降法来求的。
总之,可以看出这是一个有两个目标的优化问题,通过一个λ参数控制二者的比例,同时优化两个方面,虽然两个方向上都不会最优,但是可以兼顾两个方面的效果,即最后得到的label distribution(LD)既逼近logical label,同时相似样本之间的LD也是类似的。
# 各个方法结果对比:
作者主要使用了两种方法进行效果对比:
- 从logical label恢复到原本的label distribution的水平
- 利用得到的label distribution来训练LDL模型看预测效果
对于恢复效果,有一个自制三维数据集的可视化:
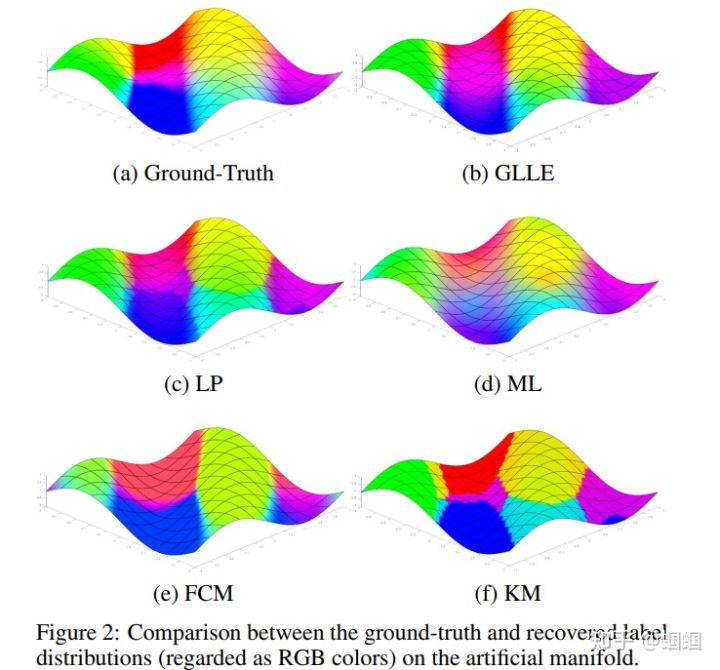
可以看出,GLLE和LP都比较接近ground truth了。
另外在其他数据集上,作者通过计算相似度来衡量使用各个LE方法来进行模型训练的效果:
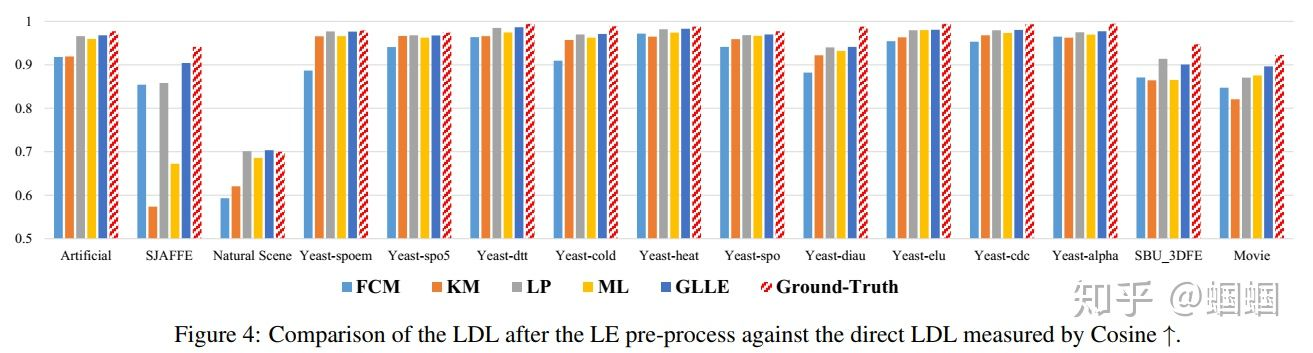
还有一个平均排名:
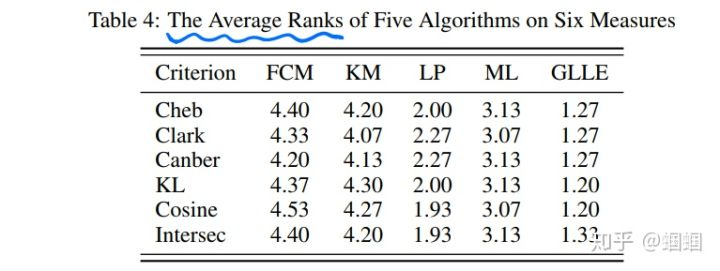
看完了这些实验结果,我最大的感觉就是:
LP这个方法真好的!又简单,效果又好!(基本比复杂的GLLE差不了多少,而且GLLE这个λ调参估计挺麻烦的) 但是GLLE的方法,其实也给了我们很多启发,毕竟相比于LP这种无监督的方法,有监督的方法肯定灵活性更强,所以取得效果的提示也是很正常的。
