# 使用Dropout解决推荐系统冷启动问题(NIPS-17)
# 推荐系统回顾 & 冷启动问题
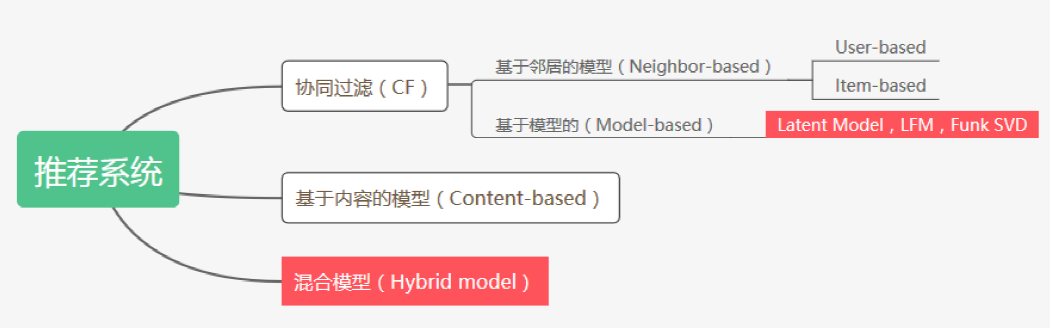
推荐系统的主流算法分为两类:基于记忆的(Memory-based,具体包括User-based和Item-based),基于模型的(Model-based)和基于内容的(Content-based)。在基于模型的方法中,**隐模型(Latent Model)**又是其中的代表,并且已经成为大多数推荐系统的选择,例如基于矩阵分解的LFM(Latent Factor Model)。
LFM主要依靠Users和Items形成的**偏好矩阵(Preference Matrix)**来估计出一个可以补全原偏好矩阵的两个分解矩阵。这种方法简单有效,而且因为分解出来的矩阵大小远远小于原矩阵,所以也十分节省存储空间。
但是,以LFM为代表的利用Users和Items的交互信息来进行推荐的隐模型,矩阵越稀疏,效果就会越差,极端情况就是,来了一些新的User或者Item,它们压根没有任何历史交互信息,即冷启动(Cold Start)问题,这时LFM就真无能为力了。因此,不少的方法开始利用Users和Items的内容信息(Content)来辅助解决冷启动问题,跟之前的LFM结合起来,形成Hybrid model。甚至有一些模型完全使用基于内容的方法(Content-based)来进行推荐。然而,Hybrid的方法,使得模型拥有多个训练目标函数,使得训练过程变得十分复杂;而完全基于内容的方法,在实证检验中被发现,性能远远不如Memory-based的方法。
本文介绍的一篇论文,提出了一种借用神经网络中的Dropout的思想,来处理冷启动问题,想法十分新颖而有趣。而且,本文提出的一种模型,可以结合Memory和Content的信息,但是只使用一个目标函数,即拥有了以往Hybrid model的性能,还解决了冷启动问题,同时大大降低了模型训练的复杂程度。

# Ⅰ. 论文主要思想
前面讲了,要处理冷启动问题,我们必须使用content信息。但是想要整个系统的推荐效果较好,我们也必须使用preference信息。目前最好的方法,就是二者结合形成的Hybrid方法,但是往往有多目标函数,训练复杂。于是本文的作者就想:
如何把content和preference的信息都结合起来,同时让训练过程更简单呢?
作者们想到,冷启动问题,就相当于一种数据缺失问题。而数据缺失的问题又可以使用Dropout来进行模拟。
因此,针对冷启动问题,本文不是引入额外的内容信息和额外的目标函数,而是改进整个学习过程,让模型可以针对这种缺失的输入来训练。
# Ⅱ. Notations
我们先定义一些notations:
代表的是个user的集合;
代表的是个Item的集合;
和形成的的preference矩阵为,而代表的是用户对项目的preference,即的第行第列。
对于一个新的User或者Item,就有。
这些都是preference的信息。接下来定义content信息:
说了半天content,到底是啥?对于user来说,content可以是user的个人资料,如性别年龄个人评价等等,也可以是其社交网络的信息,对于item,content可以是一个商品的基本信息,如产地、类型、品牌、评论等等,也可以是相关的视频图片资料。总之,content可以是通过各种渠道获取的额外信息,信息越多,当然对推荐的贡献也会越大。
来自各种渠道的多种类的信息,为了便于处理,我们统一表示成定长的向量,具体方法多种多样,比如通过一个DNN来形成,或者使用训练好的词向量等等。
我们定义: user和item得到的content feature分别为和, 则()就代表用户u(项目v)的content向量。
我们的目标就是使用 , 和 来训练一个准确又鲁棒的模型。
# Ⅲ. 模型框架 & 训练方法
前面讲过,我们是使用,和来训练模型,R如何输入呢?直接的想法就是把R的每一行每一列作为Users和Items的preference向量输入,但是由于Users和Items数量太大了,难以训练。这个时候,之前的LFM就派上用场了。我们先把R分解成两个小矩阵U和V,我们可以认为,U和V相乘可以基本重构R,涵盖了R的绝大部分信息。所以,在preference方面,我们使用U和V来代替R作为模型的输入。
即
我们对于用户u,输入是;对于项目v,输入是,然后分别输入一个深度神经网络中,得到用户u和项目v各自的一个新的向量和。
用新得到的u和v的向量和,我们可以接着相乘得到一个R的新的估计.
框架图如下:
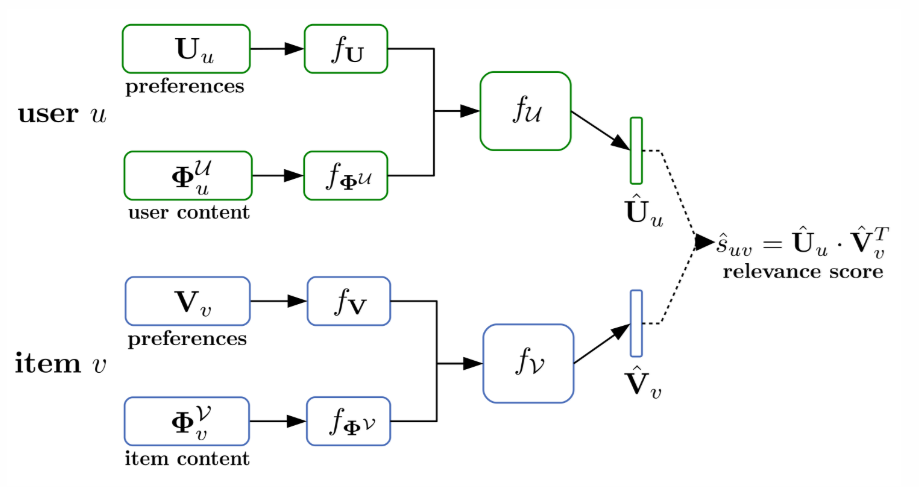
定义我们的目标函数为:
这个目标函数一开始不大理解,直接从公式看,就是希望我们训练出来的两个user和item的向量尽可能拟合原来的向量。可以看做是通过Latent Model得到的,而可以看做是通过一个深度神经网络DNN得到的。所以目标函数就是缩小Latent Model与DNN的差异。而Latent Model的结果是固定的,DNN是依靠我们训练的,所以是以Latent Model为标杆来训练的。
后来读完全篇之后,才明白,在训练的时候,我们选择的和都是有比较丰富的preference信息的向量,**在实际推荐中,如果preference信息比较丰富,那么我们只利用这些信息就可以得到很好的推荐效果。**我们在冷启动时利用content信息,也是希望能够达到有preference信息时候的性能。所以,当我们有充足的preference信息的时候,训练出的模型给予ntent内容的权重会趋于0,这样就回归了传统的Latent Model了。
在训练时,为了模拟冷启动问题,我们会按照一定的抽样比例,让user或者item的preference向量为0,即或者为。所以,针对冷启动,其目标函数为:
这个时候,由于preference向量的缺失,所以content会竭尽所能去担起大任,从而可以逼近Latent Model的效果,这也是我们的目的:preference不够,content来凑。
从上面的分析可以看出,仅仅使用一个目标函数,这个模型就可以一箭双雕:设置dropout的时候,鼓励模型去使用content信息;不设置dropout的时候,模型会尽量使用preference信息。另外,本身Dropout作为一种正则化手段,也可以防止模型过拟合。
上面解释了模型在热启动和冷启动时是怎么处理的。此外,文章还提出了在冷启动后,用户或者项目开始产生少数的preference信息的时候应该怎么处理,这样才能让不同阶段无缝衔接。
以往处理这种准冷启动问题也很复杂,因为它既不是冷启动,但是可用的preference信息也十分稀少。而更新一次latent model是比较费时的,不能说来一些preference信息就更新一次,再来推荐。所以本文给出了一种简单的方法,用user交互过的那少数几个item的向量的平均,来代表这个user的向量。他们称这个过程为transformation。所以,用户有一些交互之后,先这样transform一下,先拿去用,后台慢慢地更新latent model,等更新好了,再换成latent model来进行推荐。
所以,作者在模型训练的时候,还增加了这样的一个transform过程。
这样,整体的训练算法就是这样的:

# Ⅳ. 实验 & 结果展示
训练过程是这样的,我们有N个users和M个items,所以理论上可以形成N×M个样本。
设定一个mini-batch,比如100,每次抽100个user-item pair,设定一个dropout rate,例如0.3,则从100个用户中选出30个pair。对于这30个pair,我们轮流使用dropout和transform来处理后输入DNN,其余的70个则直接输入DNN。
接下来看看实验。
实验使用的数据集是一个科学文章数据库,用户可以在上面收藏各种文章,系统也会向用户推荐文章。
文章的content向量是tf-idf向量,用户由于没有content信息因此忽略了。另外,preference矩阵稀疏程度达到99.8%,因为平均每个用户收藏文章30多篇,而数据集中有一两万篇文章。
看看效果:
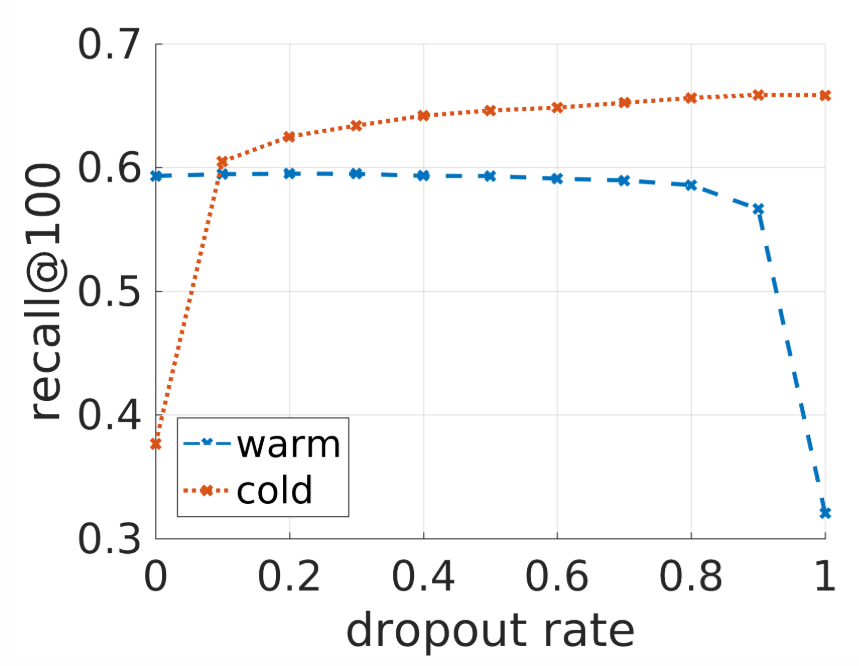
可以看出来cold start问题中,使用dropout可以大大提升推荐性能。但是过高的dropout rate会影响warm start的性能。
另外,作者也将模型和之前的一些模型做了对比,其中:
CTR和CDL是hybrid model,WMF是latent model,DeepMusic则是一个content model。
作者还提到他们模型的另一大优点就是,可以轻松地结合到之前的其他模型上,所以,作者将它们的模型和WMF以及CDL结合,称为DN-WMF和DN-CDL。对比如下:
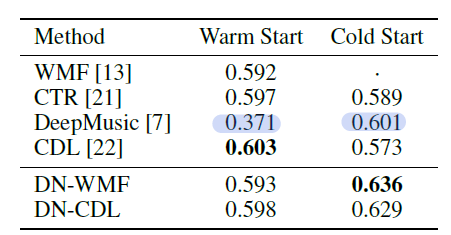
可以看到,在cold start中,DN-WMF取得了最佳效果,而且DN-WMF和DN-CDL都超过了之前的模型。这个不意外。
在warm start中,DN-WMF和DN-CDL稍稍逊色于以往的模型,这时hybrid model取得了最佳效果,但是确实差距很小。但是考虑到DN-WMF和DN-CDL的模型比hybrid模型简单地多,所以基本扯平。
值得注意的是这个DeepMusic,这是一个纯content-based model,意思是不使用preference信息。可以看到,在warm start这种有着丰富preference信息的环境下,它的效果远不如利用preference的其他模型。而在cold start这种没有preference信息的情况下,效果就超过了hybrid model。这个时候WMF这种纯靠preference根本不能算了。这也就解释了,为什么前面的目标函数要以preference-based的latent model为标杆了。
在另外一个数据集上的结果这里直接放出,就不赘述了: