# 不同损失函数的噪音免疫力

前言：今天分享一篇有一点儿意思的文章（的一部分），探究损失函数在何种情况下，会有“噪音免疫力”。最重要的一个结论就是：MAE损失，即平均绝对误差，是噪音鲁棒的，而我们最常用的交叉熵则容易受到噪音的影响。

论文标题：Robust Loss Functions under Label Noise for Deep Neural Networks
会议/期刊：AAAI-17
团队：Microsoft, Bangalore; Indian Institute of Science, Bangalore

# 一、前提知识

定义0——噪音、对称噪音、非对称噪音：

噪音：在这里指的是标签错误的样本。例如在通过众包进行数据打标的场景中噪音就是一个不可避免的问题。
对称噪音（symmetric/uniform noise）：所有的样本，都以同样的概率会错标成其他标签；
非对称噪音（asymmetric/class-confitional noise）：不同类别的样本，其错标的概率也不相同。

定义1——损失函数的抗噪性：

如果一个损失函数，在有噪音的情况下，其风险最小化的模型（minimizer）跟没有噪音时是相同的，就称这个损失函数是抗噪的（noise-tolerant）。换言之，有噪音的情况下的最优模型，跟没噪音一样。（听起来是不是不可能？）

定义2——损失函数的对称性：

我们设模型 $f(x)$ 的损失函数为 $L$ ，设分类问题的类别有 $k$ 类，则称这个损失函数 $L$ 是对称的，当它满足下面的公式：

$\sum_{i=1}^{k} L(f(\mathbf{x}), i)=C, \forall \mathbf{x} \in \mathcal{X}, \forall f$

# 二、重大发现：有对称性的损失函数，具有一定的抗噪能力

作者通过推导以及实验，发现拥有对称属性的损失函数，对噪音的抵抗能力也更强。甚至，当噪音时对称噪音时，该损失函数理论上是完全抗噪的。

# 1.理论推导：

下面我们来推导一下：

首先假设我们面对的是对称噪音，噪音比为 $\eta$ . 设一个模型在没有噪音时的目标函数 $R_{L}$ ，即损失函数在所有训练样本上的期望：

$R_{L}(f)=\mathbb{E}_{\mathbf{x}, y_{\mathbf{x}}} L\left(f(\mathbf{x}), y_{\mathbf{x}}\right)$

然后，设该模型在当前有噪音的情况下，目标函数是 $R_{L}^{\eta}$ ，公式为：

$R_{L}^{\eta}(f)=\mathbb{E}_{\mathbf{x}, \hat{y}_{\mathbf{x}}} L\left(f(\mathbf{x}), \hat{y}_{\mathbf{x}}\right)$

那么，如果损失函数是对称的，我们可以有以下推导：

即可以得出结论：

$R_{L}^{\eta}(f)=A+\alpha R_{L}(f)$

其中 $A$ 为常数， $\alpha$ 为跟噪音比 $\eta$ 和类别 $k$ 相关的系数。

由此可以知道，当 $\alpha > 0$ 的时候（即当 $\eta<\frac{k-1}{k}$ 时）， $R_{L}^{\eta}(f)$ 和 $R_{L}(f)$ 是线性相关的，故他们的f的最优解也是一样的！而只需要满足对称噪音的噪音比 $\eta<\frac{k-1}{k}$ 即可。

这相当于，在二分类问题中噪音比不超过50%，三分类问题中噪音不超过66%，十分类问题中噪音不超过90% ，都跟没噪音一样！

# 2.基于直觉的理解：

推导出上面的结论，我当时也十分的惊讶，居然这么神奇。我们想一想，上面的结论中，最重要的假设是什么？有两方面：

①损失函数自身的对称属性

这个属性直观的理解，可以通过下图：

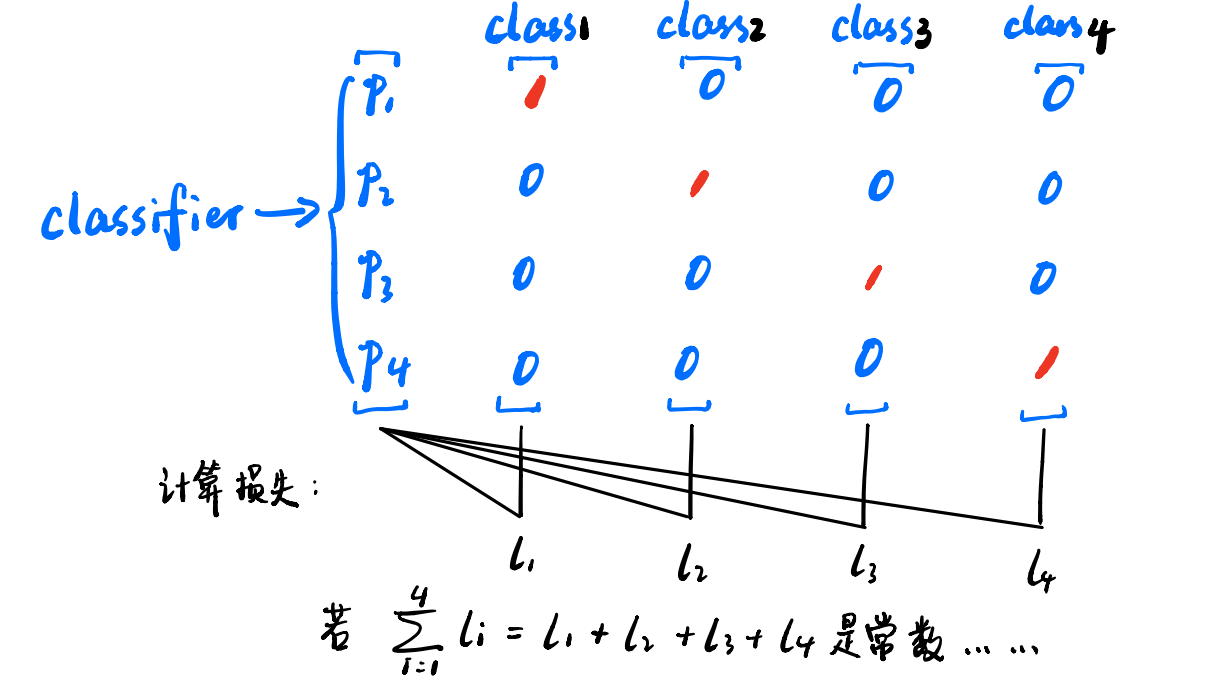
上图展示了一个四分类问题，损失函数对称，就意味着如果一个样本，它的真实标签把所有标签都遍历一遍，计算其损失之和，这个和是个常数。

②对称噪音

即当一个样本错标时，它被分配到任意一个标签的概率都是相同的。

在这样的情况下，噪音的出现，在某种意义上，相当于一个样本把所有标签都遍历了一遍。那么对整体的损失函数，只不过是增加了一个常数，因此不影响最终的优化结果。

# 3.现实的例子

通过上面的神奇的发现，我们不禁想问，拥有这么神奇的属性的损失函数应该很少见吧。其实不是，常见的MAE（mean absolute error，平均绝对误差），就是一个典型的拥有对称性的损失函数。而我们最最常用的CCE（categorical cross-entropy loss，交叉熵损失函数）、MSE（mean squire error，均方误差），则是非对称的。

下面是他们的损失函数：

$L\left(f(\mathbf{x}), \mathbf{e}_{\mathbf{j}}\right)=\left\{\begin{array}{ll} \sum_{i=1}^{k} e_{j i} \log \frac{1}{u_{i}}=\log \frac{1}{u_{j}} & \mathrm{CCE} \\ \left\|\mathbf{e}_{\mathbf{j}}-u\right\|_{1}=2-2 u_{j} & \mathrm{MAE} \\ \left\|\mathbf{e}_{\mathbf{j}}-u\right\|_{2}^{2}=\|u\|_{2}^{2}+1-2 u_{j} & \mathrm{MSE} \end{array}\right.$

通过遍历类别求和，验证其对称性：

$\sum_{i=1}^{k} L\left(f(\mathbf{x}), \mathbf{e}_{\mathbf{i}}\right)=\left\{\begin{array}{ll} \sum_{i=1}^{k} \log \frac{1}{u_{i}} & \mathrm{CCE} \\ \sum_{i=1}^{k}\left(2-2 u_{i}\right)=2 k-2 & \operatorname{MAE} \\ k\|u\|_{2}^{2}+k-2 & \mathrm{MSE} \end{array}\right.$

可以看出，MAE确实具有对称性。

作者在MNIST和RCV1数据集上做了一些实验，见下图：

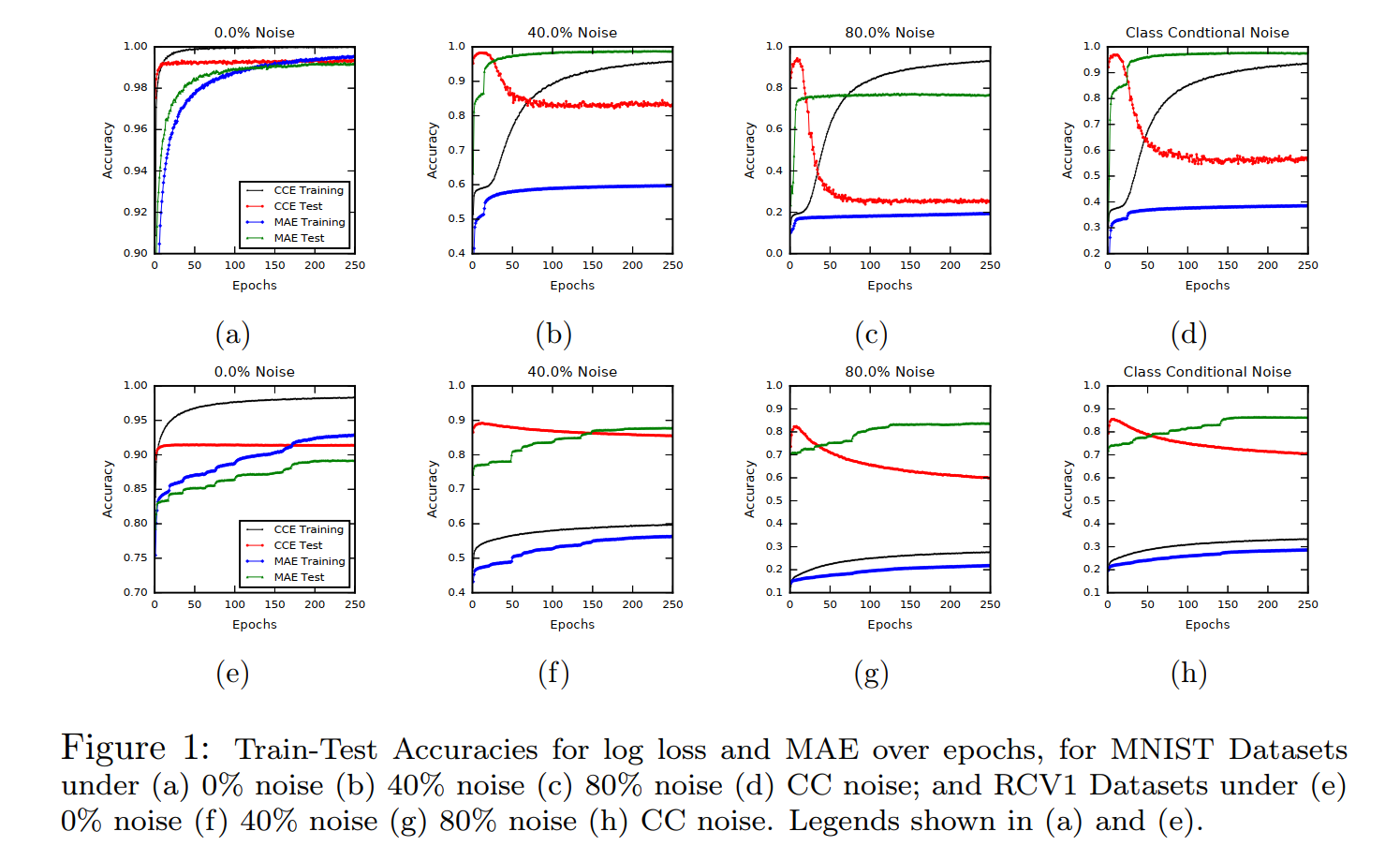
可以看出，在有噪音的情况下，CCE最大的特点就是，测试集上的accuracy像坐过山车一样，很快到达坡顶，然后飞流直下。而MAE在测试集上则是缓缓地爬坡，没有明显的下降趋势。

当然，熊掌鱼翅不可兼得，MAE自然也有其缺点，其收敛十分艰难，从图中可以看出，它在训练集上的收敛速度很慢，甚至严重欠拟合。

今天这个短短的分享就到这里。其实这个论文的分享，主要是为了下一篇更有意思的论文《Normalized Loss Functions for Deep Learning with Noisy Labels》做铺垫，这个论文给出了一个更加惊人的结论：任何的损失函数，都可以构造成噪音鲁棒的！感兴趣的读者请听下回分解~