郭必扬的写字楼

# CS224n笔记[6]:更好的我们，更好的RNNs

作者：郭必扬

上一节我们介绍了语言模型，并由此引入了RNN这种神经网络。本文我们主要讨论经典RNN网络的一些问题，从这些问题出发，我们学习一些更好的RNN结构，包括LSTM和GRU。

# 梯度消失和梯度爆炸问题（vanishing/exploding gradients）

让我们首先回顾一下RNN这种链式结构：

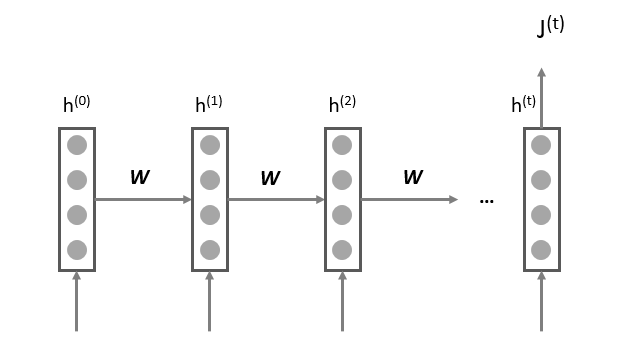
我们称这个经典的RNN结构，为vanilla RNN或者simple RNN，这个vanilla的意思是“普通的，毫无特色的”，在论文中我们会经常看到。

当我们需要对第j步的损失J(j)J^{(j)}对前面的某一步（比如h(i)h^{(i)}）求梯度的时候，通过链式法则，我们应该这样求：

∂J(j)∂h(i)\nonumber=∂J(j)∂h(j)⋅∂h(j)∂h(j−1)⋅∂h(j−1)∂h(j−2)...∂h(i+1)∂h(i)\nonumber=∂J(j)∂h(j)⋅Πi<t≤j∂h(t)∂h(t−1)\nonumber\begin{align} &\frac{\partial J^{(j)}}{\partial h^{(i)}} \nonumber \\ &= \frac{\partial J^{(j)}}{\partial h^{(j)}} \cdot \frac{\partial h^{(j)}}{\partial h^{(j-1)}} \cdot \frac{\partial h^{(j-1)}}{\partial h^{(j-2)}}... \frac{\partial h^{(i+1)}}{\partial h^{(i)}}\nonumber \\ &= \frac{\partial J^{(j)}}{\partial h^{(j)}} \cdot \Pi_{i < t \le j} \frac{\partial h^{(t)}}{\partial h^{(t-1)}}\nonumber \\ \end{align}

其中，对于∂h(t)∂h(t−1)\frac{\partial h^{(t)}}{\partial h^{(t-1)}}，我们如果忽略掉激活函数，则可以近似认为∂h(t)∂h(t−1)=W\frac{\partial h^{(t)}}{\partial h^{(t-1)}}=W，W即那个共享的权重矩阵。

则

∂J(j)∂h(i)=∂J(j)∂h(j)⋅Wj−i\nonumber\begin{align} \frac{\partial J^{(j)}}{\partial h^{(i)}} = \frac{\partial J^{(j)}}{\partial h^{(j)}} \cdot W^{j-i} \nonumber \\ \end{align}

可以看出，当W很小或者很大，同时i和j相差很远的时候，由于公式里有一个指数运算，这个梯度就会出现异常，变得超大或者超小，也就是所谓的“梯度消失/梯度爆炸”问题。

那梯度消失和梯度爆炸时分别有什么问题呢？

  • 梯度消失时，会让RNN在更新的时候，只更新邻近的几步，远处的步子就更新不了。所以遇到“长距离依赖”的时候，这种RNN就无法handle了。
  • 梯度爆炸时，会导致在梯度下降的时候，每一次更新的步幅都过大，这就使得优化过程变得十分困难。

# 如何解决vanilla RNN中的梯度消失、爆炸问题

# 梯度爆炸问题的解决

前面讲到，梯度爆炸，带来的主要问题是在梯度更新的时候步幅过大。那么最直接的想法就是限制这个步长，或者想办法让步长变短。因此，我们可以使用“梯度修剪（gradient clipping）”的技巧来应对梯度爆炸。cs224n中给出了伪代码：

从伪代码看，这个思路相当的简洁明了：当步长超过某阈值，那就把步长缩减到这个阈值。

# 梯度消失问题的解决

那么如何解决梯度消失的问题呢？梯度消失带来的最严重问题在于，在更新参数时，相比于临近的step，那些较远的step几乎没有被更新。从另一个角度讲，每一个step的信息，由于每一步都在被反复修改，导致较远的step的信息难以传递过来，因此也难以被更新。

根据hidden state的计算公式：

h(t)=σ(Whh(t−1)+Wxx(t)+b)h^{(t)}=\sigma (W_h h^{(t-1)}+W_x x^{(t)}+b)

可以看出，hidden state在不断被重写，这样的话，经过几步的传递，最开始的信息就已经所剩无几了。这根前面在讨论梯度消失的那个包含指数计算的公式是遥相呼应的，都反映了vanilla RNN无法对付长距离依赖的问题。

既然vanilla RNN无法很好地保存历史信息，那么我们能不能想办法把这个“历史的记忆”进行保存日后使用呢？————当然是可以的，LSTM就是干这事儿！

# LSTM

# LSTM扒皮讲解

LSTM这个很难记的网络，由Hochreiter和Schmidhuber这两位很难记的作者在1997年提出，主要就是为了解决RNN的梯度消失问题。论文地址：https://www.bioinf.jku.at/publications/older/2604.pdf

首先放上一张著名的著名博主colah绘制的LSTM结构图，但凡在网上搜索过LSTM的同学应该都见过：

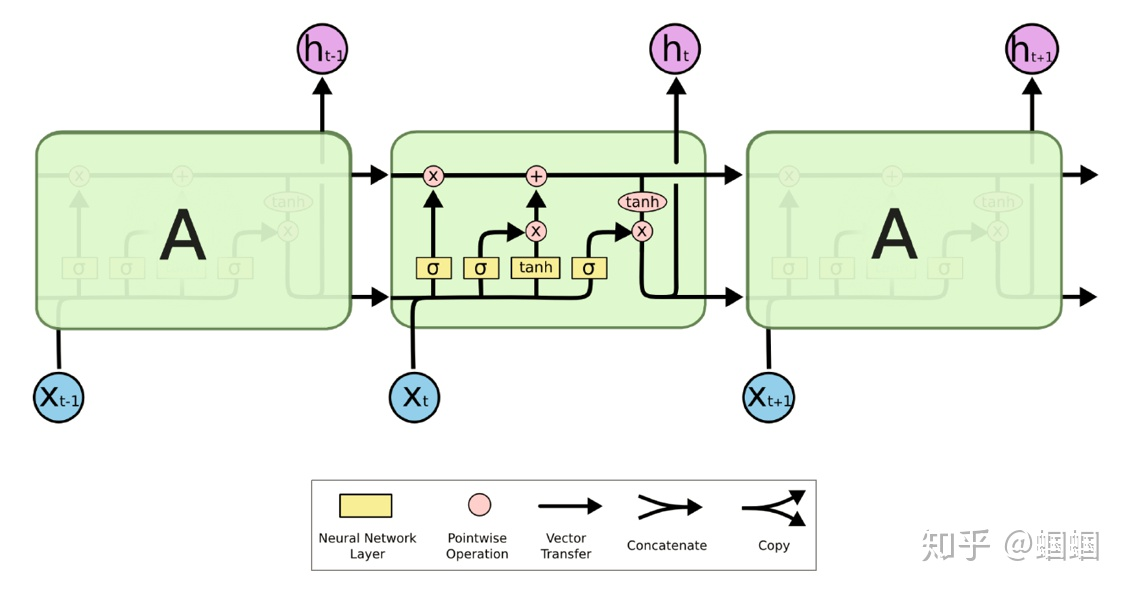
来源：http://colah.github.io/posts/2015-08-Understanding-LSTMs/

在RNN的经典结构中，每一步都会有一个隐层状态，即hidden state，我们记第t步的hidden state为h(t)h^{(t)} ，在LSTM中，作者增加了一个cell state，记为c(t)c^{(t)}。

  1. 二者是长度相同的向量，长度是一个超参数，即神经网络中的number of units；
  2. cell state中可以存储长距离的信息（long-term information）；
  3. LSTM的内部机制，可以对cell state中的信息进行擦除、写入和读取（erase,write,read）.

那LSTM是怎么实现对cell state中的信息的擦除、写入和读取呢？——有“门儿”！ LSTM有仨门儿，分别对应这三种操作。这些门有一些公共的性质：

  1. 门（gate）有什么特点呢？ —— 它可以“开”和“关”，用符号表示就是1和0，当然也可以半开半关，那就是介于1和0之间。
  2. 如何对用向量表示的信息进行“开关”呢？ —— 门也采用向量的形式，相当于一排门，来控制各个维度的信息。
  3. 如何决定“开”还是“关”呢？ —— 门的状态是动态的，根据当前的上下文来决定。

上面是介绍了门也就是gate的基本性质，下面我们来看具体有哪些门，以及具体如何控制信息流：

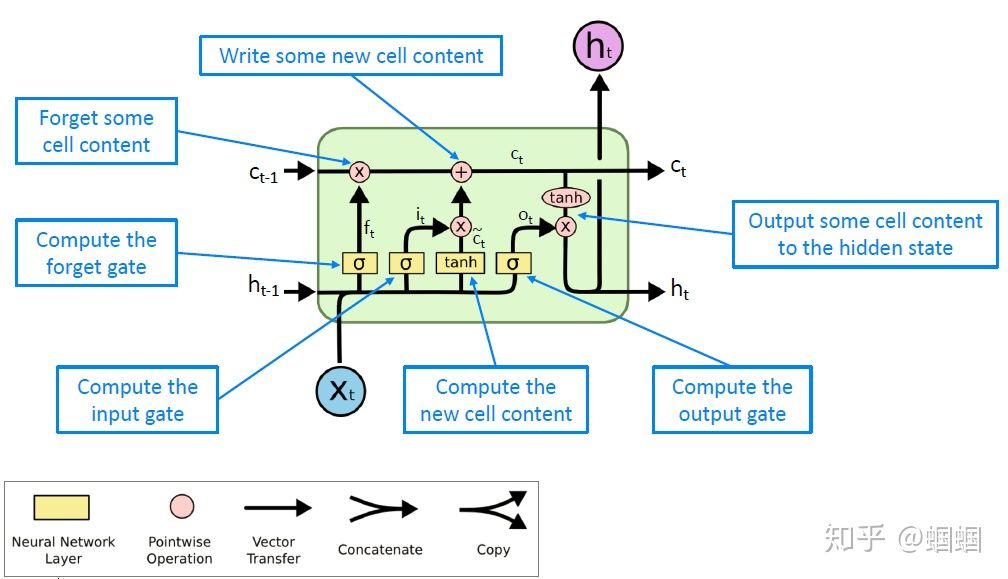
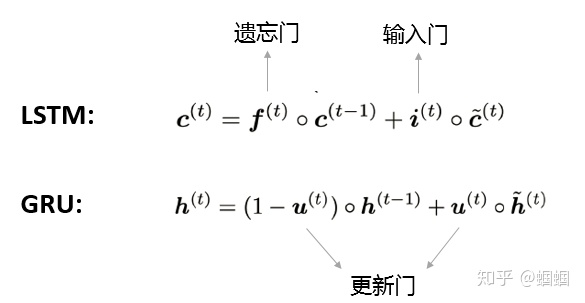
LSTM的三个门分别是：遗忘门（forget gate）、输出门（input gate）和输出门（output gate）。

  • 遗忘门：这个门，根据上一个单元的隐层状态和当前一步的输入，来“设置遗忘门的开合情况”，然后对cell state中的信息进行选择性遗忘；
  • 输入门：这个门，也是根据上个单元的隐层状态和当前的输入，来“设置输入门的开合情况”，然后决定往cell state中输入哪些信息，即选择性输入；
  • 输出门：这个门，还是根据上个单元的隐层状态和当前输入，来“设置输出门的开合情况”，然后决定从cell state中输出哪些信息，即选择性输出，输出的，就是当前这一步的隐层状态。

上面我说的应该很清楚了，不过下面这张来自CS224N的总结更加直观，大家可以对照着图片看我上面的文字：

我们对LSTM三个门的功能进行了描述，下面给出具体的模型公式，还是放出cs224n课程中的总结：

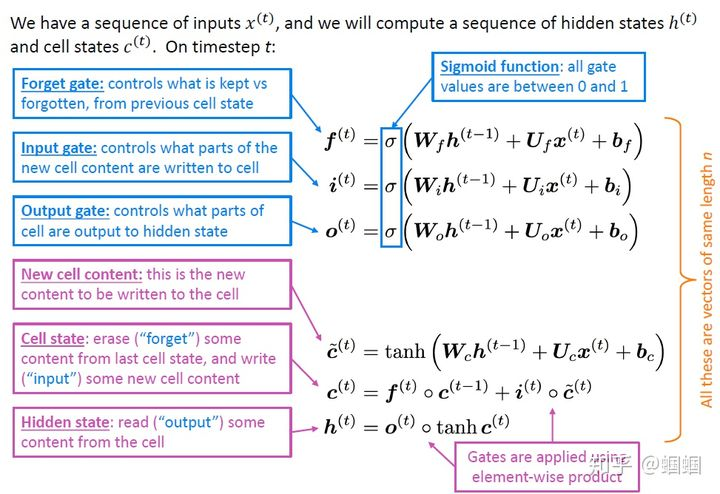
从上面的公式、我的描述以及图示中，我们可以发现，虽然LSTM结构复杂，但是很有规律的：

  1. 三个门的输入都一样！都是前一步的隐层h(t−1)h^{(t-1)}和当前的输入x(t)x^{(t)};
  2. 三个门都是针对cell state进行操作的，对上一步的cell state即c(t−1)c^{(t-1)}进行“选择性遗忘”操作；对当前步产生的信息c~(t)\tilde{c}^{(t)}“选择性输入”到该步的cell state c(t)c^{(t)}中；最后从c(t)c^{(t)}中“选择性输出”一些信息成为该步的hidden state h(t)h^{(t)}。

有没有说的很清晰？没有的话后台找我手把手教学！┗(•ω•;)┛

# LSTM为何有用

上面我们详细学习了LSTM的内部原理，现在我们讨论一下它为什么可以起作用？

RNN之所以存在梯度消失、无法处理长距离依赖的问题，是因为远处的信息经过多步的RNN单元的计算后，不断损失掉了。所以RNN一般只能考虑到较近的步骤对当前输出的影响。

LSTM相对于RNN，最大的特点就是“增设了一条管道”——cell state：

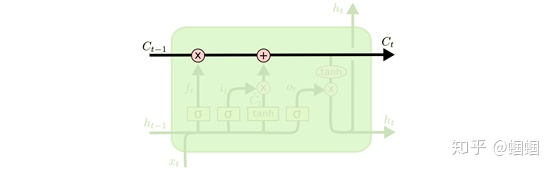
这条管道，使得每个单元的信息都能够从这里直通其他遥远的单元，而不是一定要通过一个个单元的hidden states来传递信息。这相当于卷积神经网络中常用的“skip connection”技巧。

那么信息是如何通过cell state这个管道去往诗和远方呢？通过上面的学习，我们知道，只要信息在cell state中传递时，遗忘门常开（让信息顺利通过），输入门常闭（不让新的信息进入），那么这条信息就可以像做滑滑梯一样顺流直下三千尺，想跑多远跑多远；门的这些操作，使得信息进行长距离传递成为了可能。

当然，上面说的情况比较极端，实际上，这些门一般都不会完全打开或关闭，而是处于各种中间状态。另外，是否让信息传递这么远，也是由当前的上下文决定的。所以，并不是说所有的信息都会传递老远，而是当信息真的需要进行长距离传输的时候，LSTM这种机制使得这个过程更加容易。

实际上，LSTM不光是解决了长距离依赖的问题，它的各种门，使得模型的学习潜力大大提升，各种门的开闭的组合，让模型可以学习出自然语言中各种复杂的关系。比如遗忘门的使用，可以让模型学习出什么时候该把历史的信息给忘掉，这样就可以让模型在特点的时候排除干扰。

另外，记住LSTM的各种门都是向量，长度跟hidden states一致。也就是说，这些门不是单纯对信息一刀切，而是对不同的信息的维度分别进行处理，这也就是我前面一直强调的“选择性”。

# GRU

GRU实际上是对LSTM的一个简化，它于2014年由Cho等人提出。论文地址：https://arxiv.org/pdf/1406.1078v3.pdf

这里就直接给出GRU的公式：

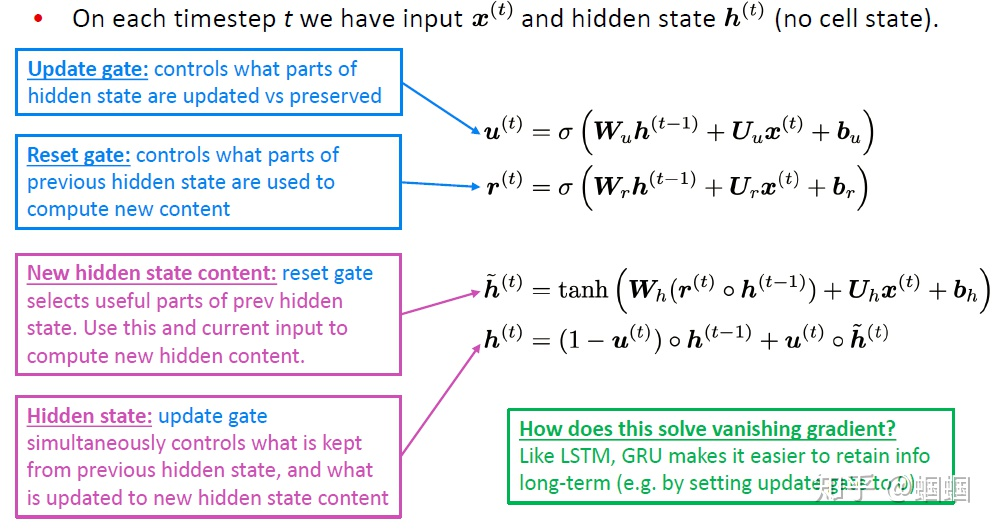
GRU也是由“门”构成的网络，它只有两个门：更新门（update gate）和重置门（reset gate）。 它主要对LSTM简化了什么地方呢？GRU在表示当前的信息的时候，只使用了一个更新门，而LSTM则使用了一个遗忘门和一个输入门：

GRU也是可以通过调整两个门的开合情况来控制历史信息的保留和当前信息的更新，从而让模型更好地应对长距离依赖和梯度消失的问题。

# LSTM vs GRU

LSTM和GRU都是著名的RNN衍生结构，一个复杂，一个简单。 一般LSTM都应该作为我们默认的选择，因为它学习能力更强，所以当我们数据量足够，又不太在乎时间开销的话，LSTM是首选。但是，如果我们很在意模型大小，训练开销，那么就可以试试GRU。

# 更多更好的RNNs

前面介绍的LSTM和GRU属于RNN单元内部的升级，在单元外部，我们可以设计一些更复杂的结构，来提高模型的综合效果。

# 双向RNNs（Bidirectional RNNs）

RNN是按照顺序处理一个序列的，这使得每个step我们都只能考虑到前面的信息，而无法考虑到后面的信息。而很多时候我们理解语言的时候，需要同时考虑前后文。因此，我们可以将原本的RNN再添加一个相反方向的处理，然后两个方向共同表示每一步的输出。

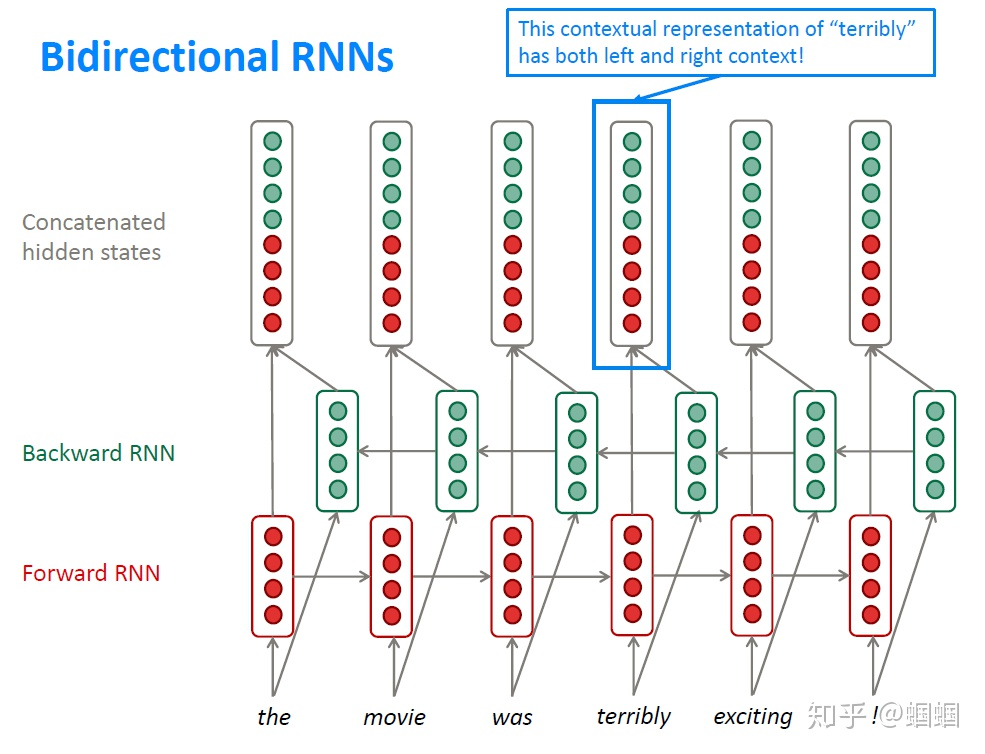
需要注意的是，只有当我们在预测时可以拿到前后文的时候，才能使用双向的模型，所以对于语言模型（LM）我们就无法使用，因为在预测时我们只有前文。但是，但我们可以利用双向的时候，我们就应该这样做，考虑更充分当然会更好。

# 多层RNN（Multi-layer RNNs）

Multi-layer RNNs也可以称为Stacked RNNs，就是堆叠起来的一堆RNN嘛。 这个更加无需更多解释，相当于神经网络加深：

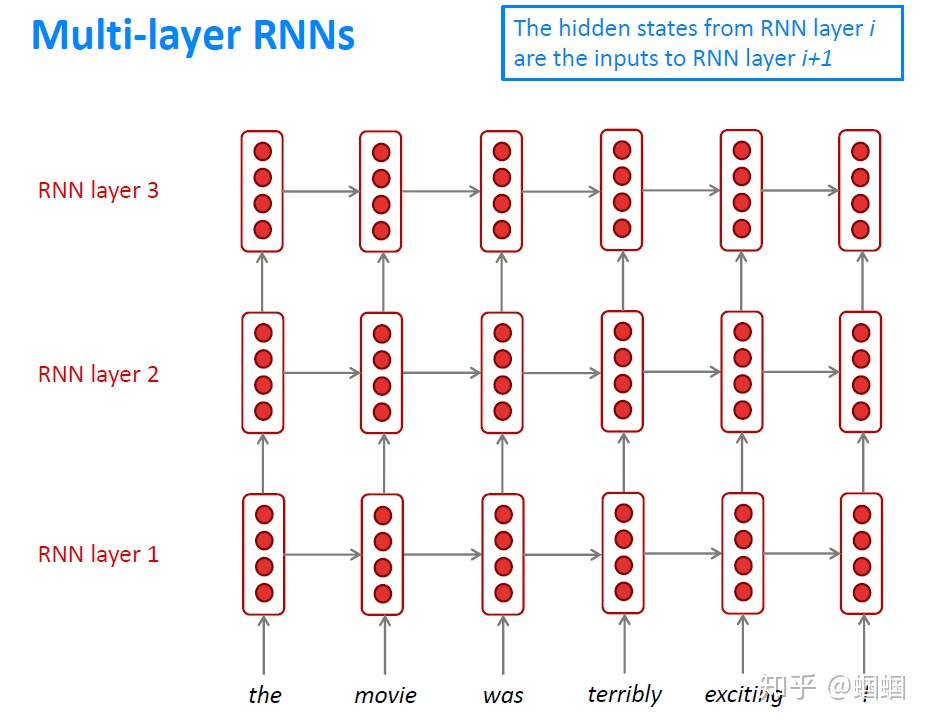
神经网络加深，往往可以带来更好的效果，因为它的学习能力大大提高。而且，就跟CNN一样，不同层次的RNN也可以学习到语言的不同层次的特征。但是，RNN跟CNN不同的是，我们无法使用太多层，一般2-4层就差不多了。

至此，我们就介绍完了RNN及其进化出来的各种结构。学习了RNN这一大类网络，我们就可以真正和NLP进行亲密接触了！(/ω＼)