CS224n笔记[3]:共现矩阵、SVD与GloVe词向量

作者：郭必扬

在上一节中我们讨论了人们对词语的几种表示方法，有WordNet这样的电子词典法，还有one-hot这样的离散表示法，后来我们介绍了Word2Vec词向量这样的低维分布式表示法。

基于共现矩阵的词向量

我们再回顾一下Word2Vec的思想：

让相邻的词的向量表示相似。

我们实际上还有一种更加简单的思路——使用词语共现性，来构建词向量，也可以达到这样的目的。即，我们直接统计哪些词是经常一起出现的，那么这些词肯定就是相似的。那么，每一个词，都可以做一个这样的统计，得到一个共现矩阵。 这里直接贴一个cs224n上的例子：

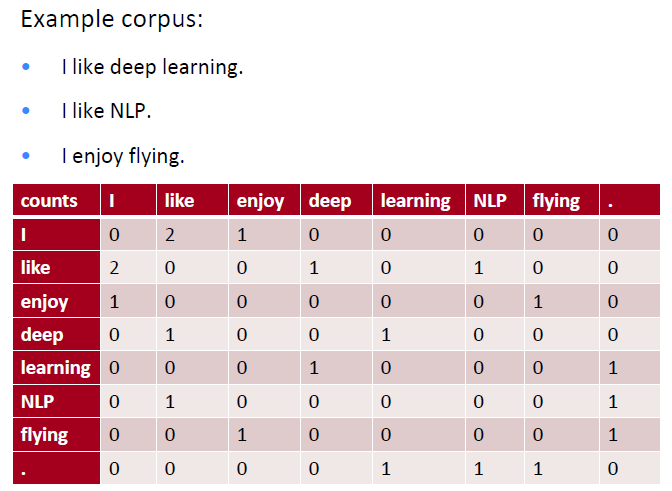
上面的例子中，给出了三句话，假设这就是我们全部的语料。我们使用一个size=1的窗口，对每句话依次进行滑动，相当于只统计紧邻的词。这样就可以得到一个共现矩阵。

共现矩阵的每一列，自然可以当做这个词的一个向量表示。这样的表示明显优于one-hot表示，因为它的每一维都有含义——共现次数，因此这样的向量表示可以求词语之间的相似度。

然后这样表示还有有一些问题：

• 维度=词汇量大小，还是太大了；
• 还是太过于稀疏，在做下游任务的时候依然不够方便。

但是，维度问题，我们有解决方法——SVD矩阵分解！ 我们将巨大的共现矩阵进行SVD分解后，只选取最重要的几个特征值，得到每一个词的低维表示。

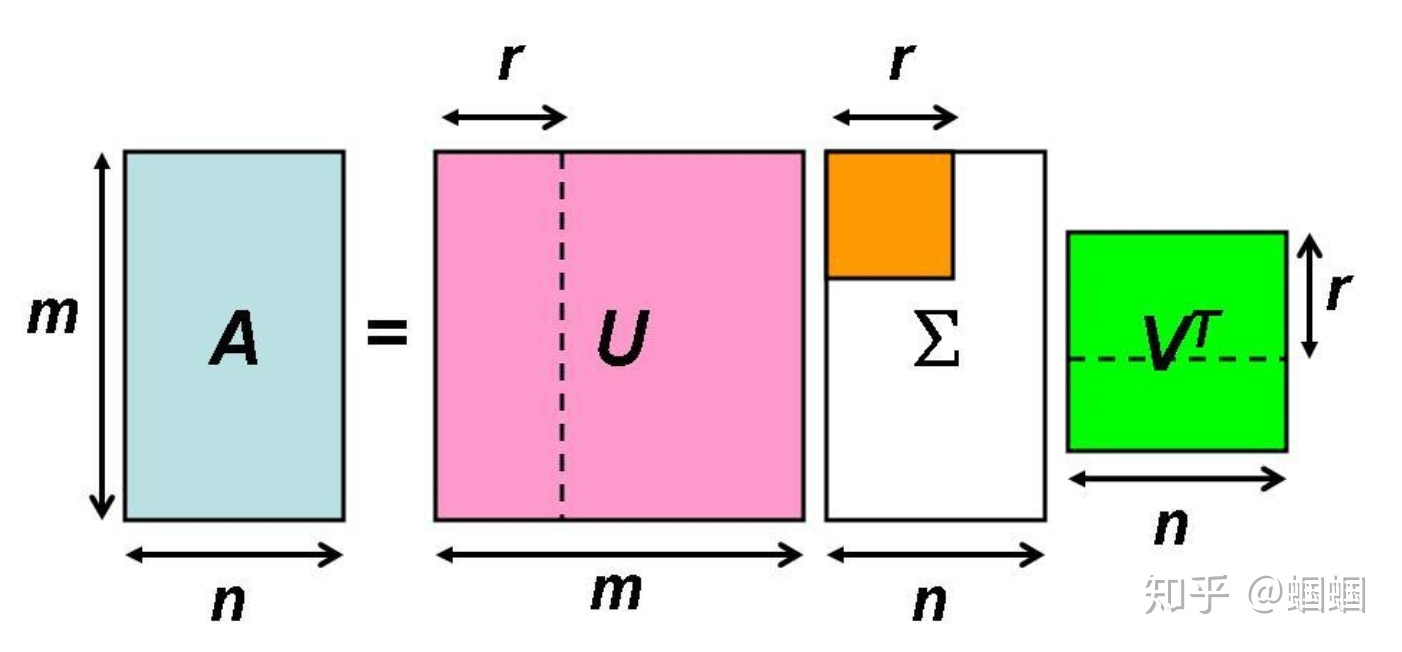
图中的A在我们的场景中就是共现矩阵，$U$、$\Sigma$、$V$就是分解出的三个矩阵。我们只选择U矩阵的前r维来作为词的向量表示。

上述的过程使用python编程十分简单，这里也是直接引用cs224n课程中的例子：

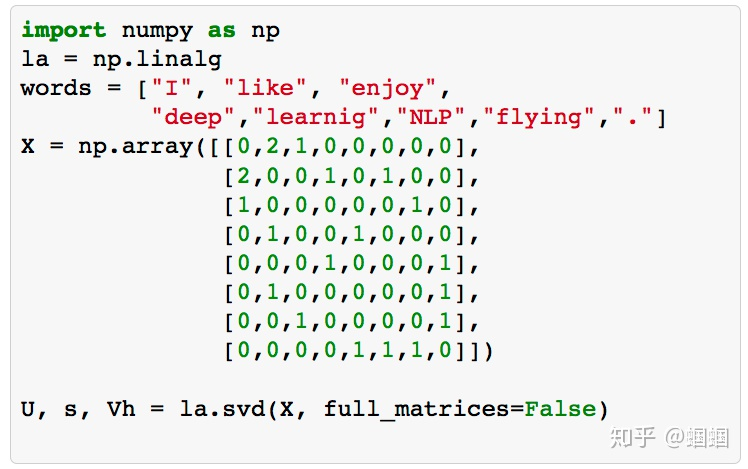
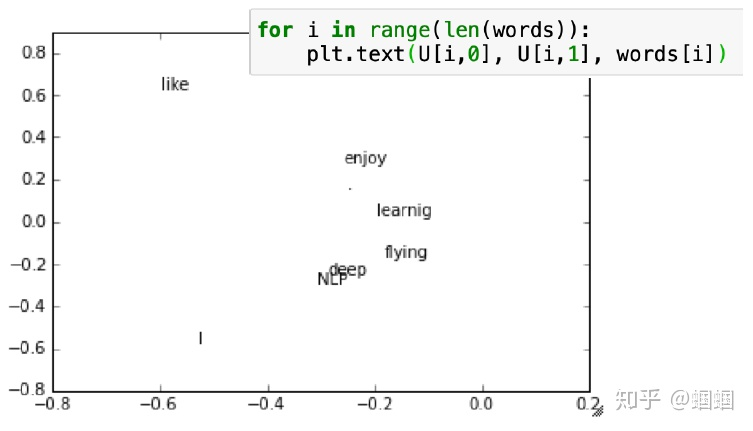
可见，即使这么简单的三句话构建的语料，我们通过构建共现矩阵、进行SVD降维、可视化，依然呈现出了类似Word2Vec的效果。

但是，由于共现矩阵巨大，SVD分解的计算代价也是很大的。另外，像a、the、is这种词，与其他词共现的次数太多，也会很影响效果。

所以，我们需要使用很多技巧，来改善这样的词向量。例如，直接把一些常见且意义不大的词忽略掉；把极度不平衡的计数压缩到一个范围；使用皮尔森相关系数，来代替共现次数。等等很多技巧。因此就有了2005年的论文《An Improved Model of Semantic Similarity Based on Lexical Co-Occurrence》提出的COALS模型。这个模型训练得到的词向量，也表现出了很多有趣的性质，跟我们熟悉的Word2Vec十分类似。

基于共现矩阵的词向量 vs. Word2Vec词向量

上面的介绍中，我们发现基于共现矩阵的词向量，也可以表现出很多优秀的性质，它也可以得到一个低维的向量表示，进行相似度的计算，甚至也可以做一定的推理（即存在man to king is like women to queen这样的关系）。 但是，它主要的问题在于两方面：

1. SVD要分解一个巨型的稀疏矩阵（共现矩阵），计算开销大，甚至无法计算；
2. 需要进行复杂麻烦的预处理，例如计数的规范化、清除常见词、使用皮尔森系数等等。

而Word2Vec的算法，不需要一次性处理这么大量的数据，而是通过迭代的方式，一批一批地进行处理，不断迭代词向量参数，使得我们可以处理海量的语料，构建十分稳健的词向量。所以在实验中，Word2Vec的表现，一般都要优于传统的SVD类方法。

但是，基于共现矩阵的方法也有其优势，那就是充分利用了全局的统计信息。因为我们进行矩阵分解，是对整个共现矩阵进行分解，这个矩阵中包含着全局的信息。而Word2Vec由于是一个窗口一个窗口（或几个窗口）地进行参数的更新，所以学到的词向量更多的是局部的信息。

总之，二者各有优劣，这启发了斯坦福的一群研究者，GloVe词向量就是在这样的动机下产生的。

GloVe词向量

GloVe是斯坦福团队来2014年提出一个新的词向量，GloVe的全名叫“Global Vectors”，重点在于这个global，即它是直接利用全局的统计信息进行训练的。

理解GloVe词向量，有两种思路：

1. 一种是由Word2Vec的skip-gram算法改进而来（思路较为清晰）；
2. 一种是由词语见的“共现概率比”构造出来（过程较为复杂）。

这里为了简便，我按照第一种思路来讲解。

GloVe会用到全局的词语之间共现的统计信息，因此我们需要首先构建共现矩阵，我们设：

• $X_{ij}$ 代表词$w_i$和词$w_j$共现的次数
• $X_i$ 代表词$w_i$出现的次数
• $P_{ij}=X_{ij}/X_i$ 代表词$w_j$出现在词$w_i$周围的概率，即共现概率

回到skip-gram算法中，我们是这样构造由中心词$w_i$预测上下文词$w_j$的概率的：

$$Q_{ij} = \frac{exp(v_i^T v_j)}{\sum^V_k exp(v_i^T v_k)}$$

其中，v就代表词向量（为了表示简便，这里也就使用一套词向量）。

这样，整体的损失函数可以写为：

$$J_{global} = - \sum^V_i \sum_{j \in context} logQ_{ij}$$

这些大家应该很熟悉了，在第一篇笔记的末尾有详细的公式介绍。

实际上，对于上面的损失函数，我们可以有一种更加高效的计算方法，因为$logQ_{ij}$会出现$X_{ij}$次，所以我们不用一个窗口一个窗口慢慢地滑动计算，而是直接把这些重复的项一起计算：

$$J_{global} = -\sum_i \sum_j X_{ij}logQ_{ij}$$

上面可以根据$X_{ij}=P_{ij}X_i$可以进一步变形：

$$J_{global} = -\sum_i X_i \sum_j P_{ij}logQ_{ij}$$

这个公式中的$\sum_j P_{ij}logQ_{ij}$我们仔细定睛一看，就会发现，这就是交叉熵嘛！

交叉熵，只是众多损失函数中的一种，而交叉熵损失函数天然有一些缺陷：由于它是处理两个分布，而很多分布都具有长尾的性质，这使得基于交叉熵的模型常常会给那些不重要、很少出现的情形给予过高的权重。另外，由于我们需要计算概率，所以必须进行合理的规范化（normalization），规范化，就意味着要除以一个复杂的分母，像Softmax中，我们需要遍历所有的词汇来计算分母，这样的开销十分巨大。

所以，我们可以考虑使用一个新的损失函数，比如——平方损失（least squares）函数，则损失函数就变为：

$$\begin{align} \hat{J} &= \sum_i X_i \sum_j (X_{ij}-exp(v_i^Tv_j))^2 \nonumber \\ &=\sum_{i,j} X_i(X_{ij}-exp(v_i^Tv_j))^2 \nonumber \end{align}$$

其中，$X_{ij}$和$exp(v_i^Tv_j)$其实就是没有经过规范化的$P_{ij}$和$Q_{ij}$。相当于我们把复杂的分母都一起丢掉了。在平方损失中，我们可以不进行规范化处理，因为我们处理的是两者之间的差异，使差异最小化，那经不经过规范化，都不影响。但是在交叉熵中就必须进行规范化了，因为我们处理的是概率。

由于$X_{ij}$的取值范围非常大，这样会不容易优化，所以我们再进行取对数处理：

$$\hat{J} = \sum_{i,j} X_i(v_i^Tv_j-logX_{ij})^2$$

最后，对于那个权重项$X_i$，其实我们可以更加优化的用一个同时依赖于i，j的函数：$f(X_{ij})$来代替，来让我们更精细地调整不同频率的词的损失。GloVe论文中f函数的图像长这样：

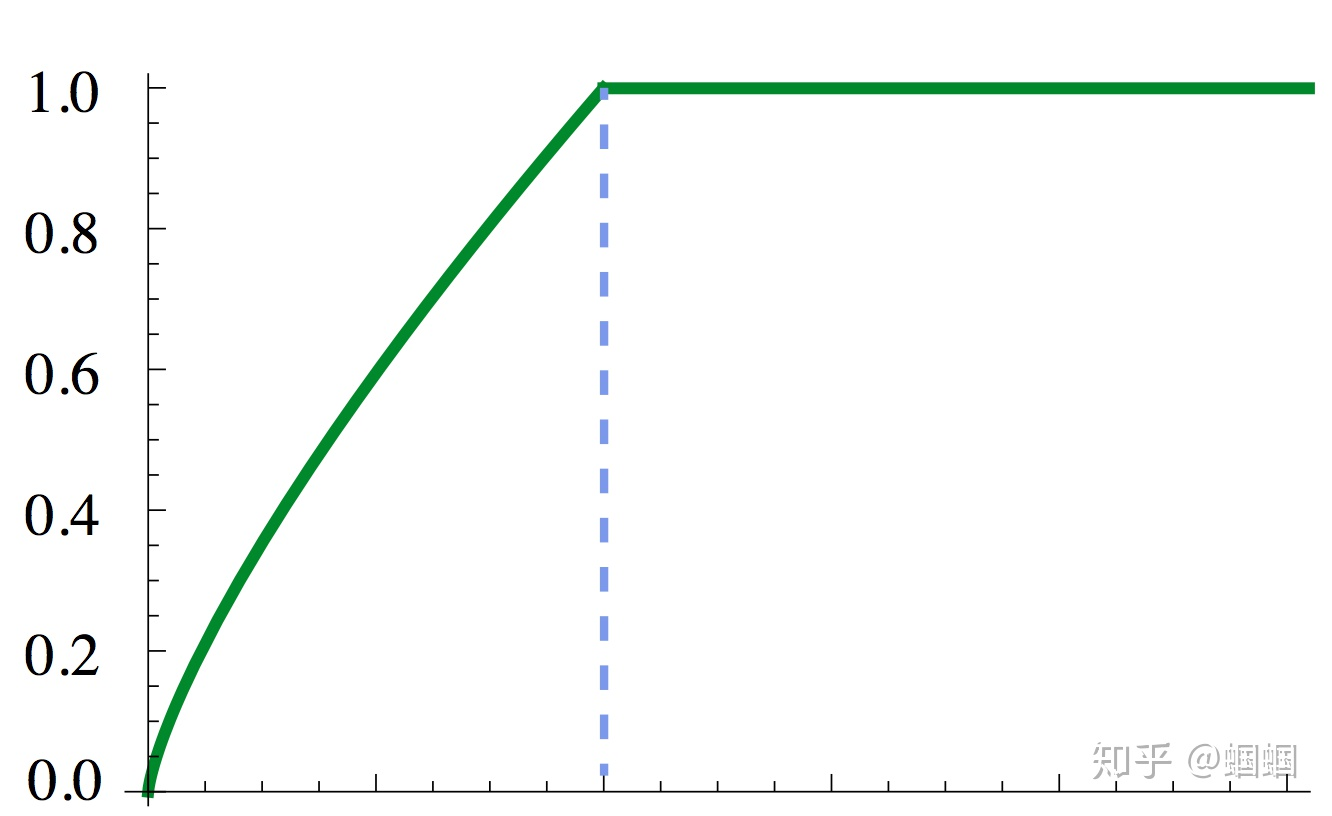
这样的函数使得过于高频的词权重不会过高。

千呼万唤始出来，我们终于得到了GloVe的损失函数：

$$\hat{J} = \sum_{i,j} f(X_{ij})(v_i^Tv_j-logX_{ij})^2$$

（当然，其实还有一点不完整，那就是我们可以在内部再添加一些偏置项，bias term，但是这个不重要了）

GloVe词向量好在哪？

上面详细讲述了GloVe词向量如何通过改进Word2Vec的skip-gram算法得来。最主要的，就是我们把交叉熵损失函数替换成了平方损失函数。这样，就明显可以让我们的计算更简单。

另外，GloVe词向量的训练，是直接面对$X_{ij}$，即共现矩阵，进行优化的。也就是它是直接朝着全局的统计信息进行训练优化的。这样有什么好处呢？

a 更充分的利用统计信息
b 充分利用语料中的大量重复信息来简化计算

第二点怎么理解？在Word2Vec中，我们是通过滑动窗口来进行计算的，我们在遍历整个语料的过程中，同样一对<中心词i，上下文词j>可能会出现在多个窗口中，这些计算我们都存在重复，而如果利用统计信息，我们可以只计算一次，然后乘以次数即可。

对于GloVe，模型的计算复杂度依赖于共现矩阵$X$中非零元素的个数，其上限为$O(|V|^2)$，而skip-gram的复杂度为$O(|C|)$。其中V是词汇量大小，C是语料库的长度，一般情况下，$|V| \ll |C| \ll |V|^2$.

但是，实际的语料中，$X$一般是十分稀疏的，非零元素相比之下是很小的。经过对实际语料的研究，我们发现GloVe的实际复杂度大概为$O(|C|^{0.8})$，显然还是小于skip-gram的复杂度的。这也进一步印证了上的第二点好处。