CS224n笔记[1]:Word2Vec从何而来

作者：郭必扬

前言：关于自然语言

人类的语言文字的出现，帮助了人类记录自己的智慧，由此加速了人类文明的进化，这也是人区别于动物的主要优势之一。

如今网络通信如此发达，相比之下，我们人类语言的传播速度是非常低下的，难道是人类的语言过时了吗？显然不是。虽然我们说话、打字的速度，永远不可能超过无线电，但是我们的大脑自己进化出了一种极为强大的自适应压缩机制，这时的我们即使使用很少的文字，也可以传递大量的信息。

在人工智能领域内有一种说法：自然语言处理是人工智能皇冠上的明珠。这说明了NLP的重要地位，但更加体现的实际上是NLP的难度。我们试图去让机器能像人一样处理、理解自然语言，但是由于人类语言的复杂多义、极度压缩的特性，我们至今仍然没能真正摘取这颗皇冠上的明珠。这也是我们学习自然语言处理技术的初衷——试图让计算机把自然语言处理地更细致一点、理解的更透彻一点，哪怕只有一点。

一、如何让计算机处理自然语言？

1.WordNet（电子词典式）

最直观的，就是把我们纸质的字典搬到电脑上，这样我们就可以很方便地查询关于这个词相关的信息。例如著名的WordNet，它被称为是NLP中的瑞士军刀，下图展示了通过调取wordnet工具包查询一个词的相关信息：

WordNet的构建花费了很多人多年时间，是对NLP领域伟大的贡献。但是我们现在实际上很少使用它了，因为它有这么几个缺陷：

a. 缺乏词汇之间的差别的刻画
b. 不能计算精确的相似度
c. 词汇永远不会完整，且难以更新

2.one-hot表示（离散表示）

后来，人们开始对词汇进行离散的表示，即one-hot表示，如下图：

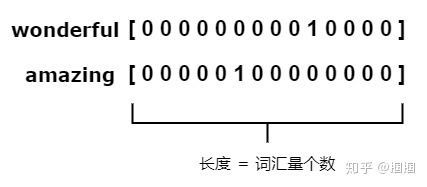
这种方式也曾一度推动了NLP中许多任务，取得了一定的效果。然后这种方式很明显有几个缺陷：

a. 词汇太多，用one-hot表示太稀疏、太费劲
b. 难以衡量词汇之间的相似度

针对上面的相似度的问题，实际上后面有人想到了使用构建词语相似度表（word-similarity table）的方式来解决，这样首先需要人工得确定每两个词的相似性程度，这显然是不可能完成的任务，那通过WordNet来获取相似度呢？这样可以小范围的实现，但是明显WordNet是很不完整的。

3.Word2Vec（低维分布式表示）

再后来，划时代的Word2Vec到来了。它主要的思想就是一句话：

一个词的意义，应该由其周围经常出现的词来表达。

这样是很有道理的，也是具有普适性的。比方在人际关系中，我们每个人实际上是什么样的人，是由我们都接触些什么样的人决定的。这个道理放到自然语言中一样是适用的。

那么如何利用这样的思想来得到词语的表示呢？ 我们可以设计这样的一个任务： 既然我们希望一个词的向量是由其上下文表示，那么就可以通过一个词去预测其周围的词。（类比：通过对你这个人的观察，来预测你的朋友圈是啥样的，搞学术的？做生意的？）

我们可以试着使用公式来表示一下： 一句话中，我们选择一个中心词（center/target word）$w_c$，设置一个窗口（window）大小$m$来选择上下文词（context）$w_o$，其中$o=c+j,-m \le j \le m, j \ne 0$。我们设使用中心词$w_t$预测其上下文的某一个词$w_o$的概率为$P(w_o|w_c)$.

我们显然希望对于真实的中心词与上下文词，这个概率值应该尽可能大，这样就说明我们可以使用一个词来预测其周围的词。

那如何表示$P(w_o|w_c)$这个概率呢？ 首先，我们需要知道，这个概率应该是词向量的函数，也就是通过中心词和周围词的词向量而求出，我们需要优化的就是这个词向量参数。

我们设词汇表中第i个词的词向量为$v_i$ ,设中心词和周围词的序号分别为$c$ 和$o$，则内积$v_o^Tv_c$可以一定程度上表示两个词的相似程度，然后我们可以使用一个Softmax函数，来将其转化成概率值，即：

$$P(w_o|w_c) = \frac{exp(v_o^Tv_c)}{\sum^{V}_{i} exp(v_i^Tv_c)}$$

但是，我们在优化时发现，上面这个式子求导不太方便，我们如果对中心词和周围词采用两套词向量分别表示,即中心词用$v_c$ 表示，周围词用$u_o$ 表示，求导就会容易很多，所以我们更常见的写法是下面这种：

$$P(w_o|w_c) = \frac{exp(u_o^Tv_c)}{\sum^{V}_{i} exp(u_i^Tv_c)}$$

于是，对于一个中心词$w_c$和一个上下文词$w_o$，其损失函数就可以由上面的概率值的负对数来表示：

$$\begin{align} J_{single} &= -log(P(w_o|w_c)) \nonumber\\ &= -log(\frac{exp(u_o^Tv_c)}{\sum^{V}_{i} exp(u_i^Tv_c)})\nonumber \end{align}$$

那么，整个窗口内损失函数，就是把窗口内各上下文词与中心词计算损失再累加：

$$\begin{align} J_{window} &= \sum_{w_o \in window}J_{single} \nonumber \\ &= -\sum_{w_o \in window}log(P(w_o|w_c))\nonumber \end{align}$$

如果要计算在整个语料中的损失，那就是再遍历所有的中心词，再累加：

$$\begin{align} J_{corpus} &= \frac{1}{V}\sum_{w_c \in corpus}J_{window} \nonumber\\ &= -\frac{1}{V}\sum_{w_c \in corpus}\sum_{w_o \in window}log(P(w_o|w_c))\nonumber \end{align}$$

其中V为词汇表大小。

这样我们就明确了我们要优化的函数，就可以通过常用优化算法进行求解，得到低维连续的分布式表示的词向量。

实际上，上面的算法，就是大名鼎鼎的skip-gram算法的核心。

通过这样的方式，我们得到的词向量，具有很多优良的性质。最直观的感觉就是，我们把一个词，表示成了一个向量，而且每一个维度都有隐藏的含义。而且，相似的词、邻近的词，其词向量表示也是相似的，可以直接通过求余弦相似度来计算任何两个词之间的相似性。 如下图，我们将训练好的词向量降维后进行可视化：

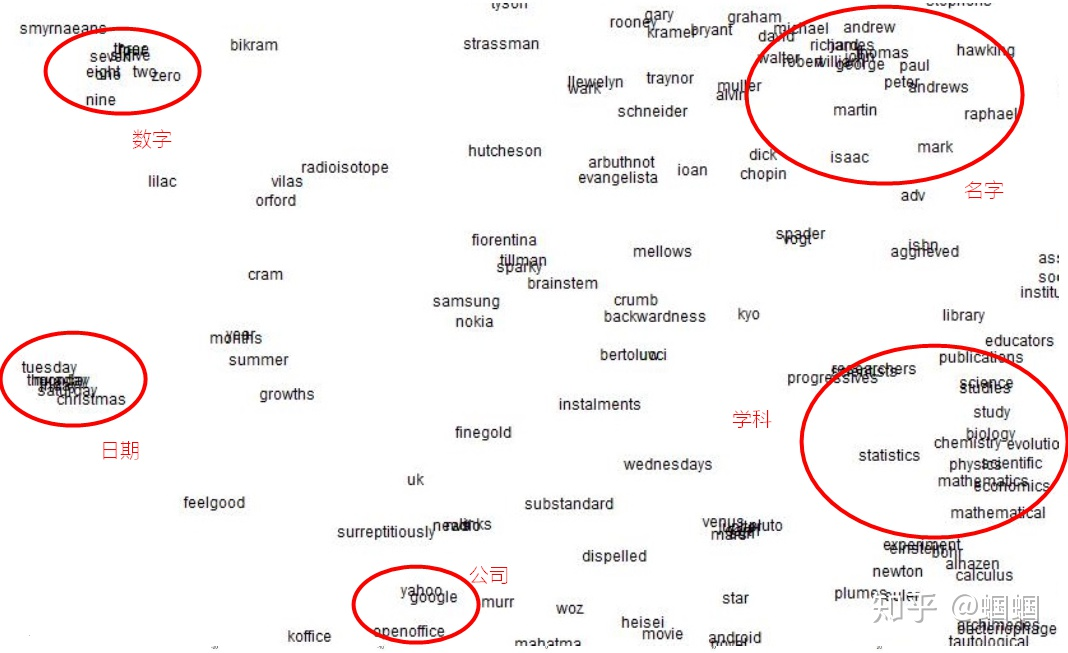
从图上可以看出一些类别的词汇明显的聚在一起。 而且，词向量甚至还可以进行线性的数学计算： 例如v(king)-v(man)+v(women)得到的词向量，最相似的就是v(queen)！

这就是词向量的不可思议之处，明明算法其实很简单很朴素，但是居然能够把语言中这么微妙的关系给捕捉到。

以上就是词向量的简介。 关于词向量方法的细节、推导、以及相关实现，请见后面的章节。