# 神经网络的前世今生
From Logistic regression to Neural netword
提纲:
传统的机器学习来做分类问题
- Logistic/Softmax regression
- 上述算法的决策边界
- 用什么损失函数
神经网络的本质剖析
- 从Logistic regression到神经网络
- 前向传播和反向传播
- 训练的注意事项(参数初始化、优化方法)
- 从神经网络的角度看Word2Vec
卷积神经网络什么鬼 ......
# 一、传统机器学习对付分类问题
# 1.Logistic Regression(二分类)和Softmax(多分类)
LR我们一般之前都接触过,就是一个用W、b对X进行线性表示,然后再通过一个非线性的激活函数输出预测值。 曾经我突然有一个问题:“不是有一个非线性的激活函数吗?为什么还是只能进行线性的分类?” 这个问题说明了我对Logistic regression 的理解十分肤浅,对分类问题的本质还是不了解。 所以我重新回顾了一下分类问题的本质是什么。
假设我们的两个类别在图上表示为:
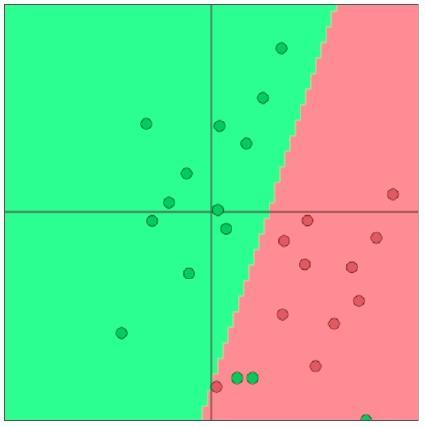
思路是什么:
- 首先观察不同类别的点的分布情况
- 找到分割开不同类别的方法(寻找切平面)
- 拟合切平面
图上的两个类,可以大致用一条直线分隔开来,我们设这个直线可以表示为:
Z = W·X + b
我们希望能够求得这条直线,或者说,想求出W和b。这样的话,WX+b>0和WX+b<0就可以吧原来的两个类给区分开了。见下图:
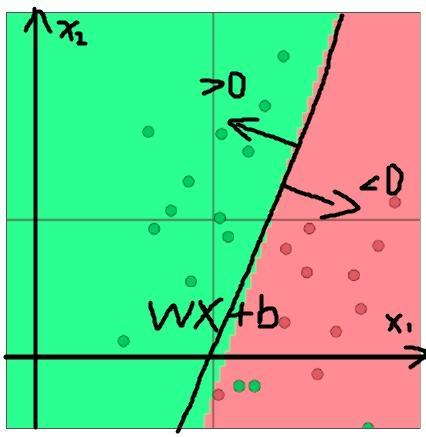
怎么学习这条直线呢?我们可以使用所有训练样本的点到直线的距离作为衡量指标,让距离尽可能大。也就是我们的最小二乘法。
但是,如果我们希望得到的结果是一个概率,即预测一个点属于各个类别的概率分布式多少。拿我们应该怎么办呢? 这个时候,我们就可以采用sigmoid函数。
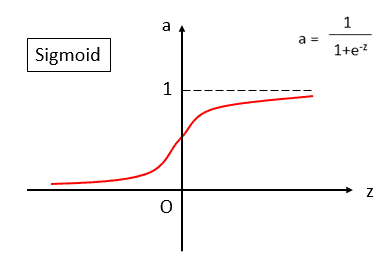
从sigmoid函数的图像可以看出,它可以把一个输入压缩到0-1之间,并且是一个中心对称图形,可以很好地拟合一个概率分布。比方我们希望某个点,属于第一类的概率为0.7,属于第二类的概率为0.3.这样似乎更符合实际一些,没那么武断。
我们把上面的Z = W·X + b作为sigmoid的输入,输出为y,则当Z>0时,y>0.5;当Z<0时,y<0.5。我们可以发现这样的结构很合理:
对于那些靠近直线Z = W·X + b的点,本来类别就比较模糊,如果直接用Z的符号来判断类别,就不大好。但是,这些靠近直线的点,由于Z的值和接近0,所以通过sigmoid输出的概率值也接近0.5,我们就可以看出那些点的分类的把握不是很大,这样就十分合理。
上面说的这些,就是所谓的Logistic Regression,表达式就是:
Z = W·X + b
y = σ(Z)
2
这样,我们的输出就是一个概率分布了。
上面讲的问题是一个二分类问题,那对于多分类我们怎么办呢?
多分类,可以转化为多个二分类,即学习多条直线的W和b:
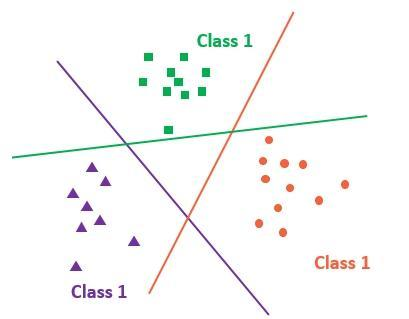
图中,每一条直线,都是用于把对应的类和其他所有的类分开,这样,有几类,就需要几条直线。 设类别为i,则每一条直线可以表示为:Zi = Wi·X + bi。这里的Wi和前面的W形状一样。
如何获得多个类别的概率分布呢?用sigmoid函数是肯定没办法了。这个时候,Softmax函数就闪亮登场了。
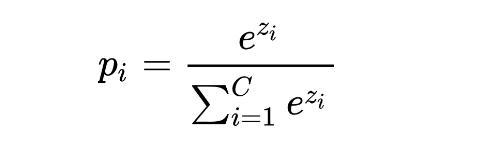
可以很容易地看到,每一类的pi加起来就是1,于是就形成了一个多类别的概率分布。
再回头看,为什么是决策边界都是线性的?因为我们预设分割边界就是线性的呀!**而sigmoid和Softmax这些非线性函数,只是起到概率分布转换的作用!**所以,决策边界自然是线性的。那个问题不攻自破了。
传统机器学习的方法怎么解决非线性问题呢?————SVM
上面介绍了Logistic/Softmax Regression,但是问题还没完,损失函数还没设定呢,那么我们应该怎么设定损失函数呢?
# 2.损失函数
开门见山吧,这里我们使用**“交叉熵(Cross-entropy)”**。主要是我们要了解,这个交叉熵到底是什么玩意儿,为什么用这种形式,以及能否用其他的损失函数?
熵的概念来源于信息论,熵说白了就是信息量。在信息论中,一件事的信息量是怎么衡量的呢?
假设事件A发生的概率为p,则定义熵(信息量)为
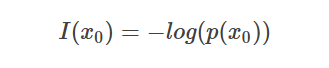
可以发现,概率p越大,熵就越小,信息量就越小。为啥呢?细细想一想也很自然,概率很大的事情,就很确定,那就跟地球是圆的一样,没什么信息量。而概率小的事情,因为不确定性很大,有很多种可能,所以信息量就大,就比如说“地球是平的”,会蕴含很多的信息。
那现在我们有一堆样本X=[x1,x2,...,xn],概率分布是p(x1),p(x2),...,p(xn).那么这些样本蕴含的平均信息量/平均熵是多大呢?很简单,求平均:
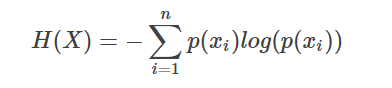
明白了上面的内容,我们接下来看一下,如果有两个概率分布p和q,怎么衡量这两个概率分布之间的差异呢?这里就使用KL散度:
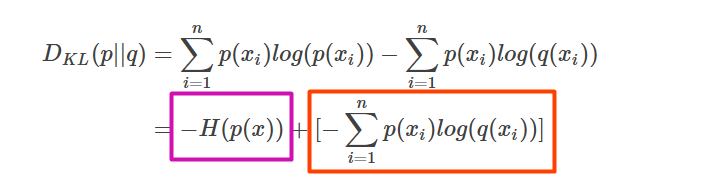
把KL散度分解一下,可以得到:
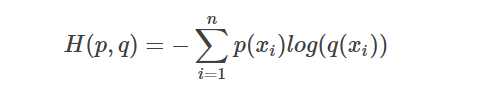
可以看到,左边的部分就是前面的概率分布p的信息量,剩下的右边的部分,就是我们传说中的交叉熵:
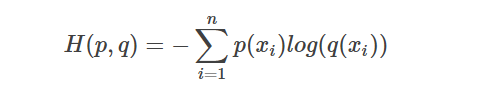
回到我们的机器学习中,假设我们样本的真实概率分布是p,我们通过模型预测出来的概率分布是q,那么我们的损失函数,就可以使用KL散度。而因为真实概率分布p是固定的,所以KL散度的第一项-H(p(x))是一个定值,可以省去,所以我们就可以只用交叉熵来作为损失函数了,它就是衡量了我们的预测分布q与真实分布p的差距。
所以,一般对于这种输出概率分布的模型,我们都采用交叉熵来作为损失函数。
Cross-entropy VS. MSE
有人问,不是还有一个著名的MSE(Mean Square Error)吗?也是经常作为回归问题的目标函数呀,它和ACE(Average Cross Entropy)比起来孰优孰劣呢?
它俩的差别其实不大,都是常用的损失函数。但是在Logistic regression以及神经网络中,我们更常使用的还是ACE。原因主要体现在求导、更新参数的过程中:
大家不妨手推一下使用MSE和ACE对参数W进行求导的公式,大致推一推便可以发现:
- MSE对W的导数,正比于sigmoid的导数,而根据sigmoid的图像可知,随着我们的训练的进行,预测值y会越来越接近0或者1,sigmoid的导数越来越小,这样会导致在梯度下降法中参数更新的速度越来越慢,可能难以收敛。
- ACE对W的导数,正比于预测的误差,误差越大,导数越大,更容易收敛。
# 二、神经网络登场
其实,理解了Logistic regression,也就基本理解了神经网络,也就大概知道了深度学习的大致思路。
我们首先用一个图表示一个Logistic regression:
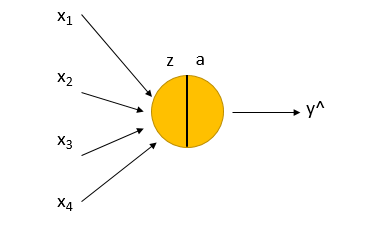
图中x1-x4为X的各个维度,Z=WX+b,a就是把Z输入激活函数sigmoid得到的结果,称为激活值(activation),然后就得到预测值y^.
如果我们把图中的那个黄色球看做一个神经元的话,那么实际上神经网络就是多了几个或者几层的神经元:
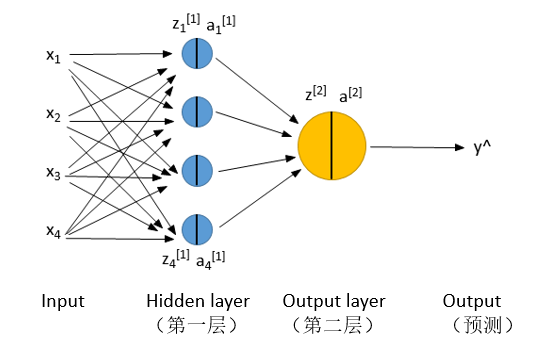
每一个神经元,内部的原理都是一样的。所以说,Logistic regression就是神经网络的基础。
多层神经网络,因为它是多个非线性函数的叠加,理论上可以拟合任意复杂的函数,这就突破了Logistic regression的局限,可以对付各种非线性问题了。
神经网络的神秘之处在于,除了最开始的输入X是我们知道意义的,中间层的各种输入输出是我们无法理解的。
但另一方面,这正是神经网络的强大之处。每一层的输入,都可以看做是对原数据提取的某些特征,然后再经过处理,提取另一些特征,再传给下一层,如此反复。这样经过学习,就可以学习到许多我们人无法定义或者不了解的特征,但是这些特征对于我们判断事务本身是有帮助的。
这样,实际上我们是让神经网络主动地从数据中发掘特征,从而减少了我们人工定义特征的工作,**“让数据说话,而不是替数据说话”。**这也正是“深度学习”的主要思想,让模型的深度赋予模型以力量,从而让模型去自动提取特征,完成我们的任务。
# 3.卷积神经网络
... (此处省略一万字,请直接参看【从此明白了卷积神经网络】一文)
