# CS224n笔记[2]:Word2Vec算法推导&实现

作者：郭必扬

其实关于Word2Vec的详细推导，我之前写过一篇十分详细精美的手写笔记：【link】，墙裂推荐阅读，个人认为写的确实不错。

本文主要根据cs224n的assignment2的计算题和编程题进行一个总结回顾。我发现这份作业设计太棒了，循序渐进，有理论有实践，前后呼应，难度适中，整个的编排我觉得更像是一份详细的教程。所以这里我就从这些题目出发，来复习、思考Word2Vec。

本文的主要内容：

使用朴素softmax损失函数的word2vec

使用负采样式损失函数的word2vec

编程实现的细节

# 一些Notations

skip-gram的目标就是学习由中心词 $c$ 预测其上下文中某特定词 $o$ 的概率 $P(O=o|C=c)$ ,o就是outside的意思，c就是center的意思。o从哪里找呢？我们需要先确定一个窗口大小window size，例如下图中，我们使用唯window size=2，那么中心词“banking”就可以找到4个上下文词：

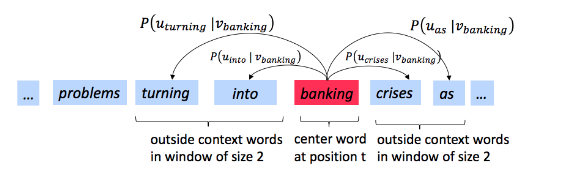
采用窗口大小为2的word2vec skip-gram算法

# 朴素softmax损失函数(Naive-Softmax Loss)

对于 $P(O|C)$ ，我们可以使用词向量的内积然后用softmax函数来构建：

$P(O=o|C=c) = \frac{exp(u_o^Tv_c)}{\sum_{w \in Vocab}exp(u_w^Tv_c)}$

这里我们对中心词c和上下文词o使用了两套词向量表示 $V$ 和 $U$ ，但注意二者形状完全一样，不是互补的关系。

这样，对于单个词对<c,o>，其损失函数可以写为：

$J_{naive-softmax}(v_c,o,U) = -logP(O=o|C=c)$

其实，该损失函数还有另一种表示方法，那就是周围词真实分布 $y$ 与预测出来的概率分布 $\hat{y}$ 的交叉熵。即：

$J_{naive-softmax}(v_c,o,U) = -\sum_{w \in Vocab} y_w log(\hat{y_w})$

# 1.证明概率的负对数损失函数等价于交叉熵损失函数

这就是作业2的第一小问。证明也十分简单：因为真实分布 $y$ 是一个one-hot向量，即只有当前真实的上下文词o的位置上，才是1。故

$\begin{align} &\sum_{w \in Vocab} y_w log(\hat{y_w}) \nonumber \\ &= 1 \times log(\hat{y_o})\nonumber \\ &=logP(O=o|C=c) \nonumber \end{align}$

即证。

# 2.计算naive-softmax loss对中心词、上下文词的导数

求导这个就不用过多的解释，就是chain rule一把梭，下面展示一下求导过程：

对中心词向量 $\boldsymbol{v}_c$ 求导：

$\begin{aligned} & \frac{\partial J_{\text {naive}-\text {softmax}}(\boldsymbol{v}_{c}, o, \boldsymbol{U})}{\partial \boldsymbol{v}_{c}} \\ &=-\frac{\partial \log (P(O=o | C=c))}{\partial \boldsymbol{v}_{c}} \\ &=\frac{\partial \log \left(\sum_{w=1}^{V} \exp \left(\boldsymbol{u}_{w}^{T} \boldsymbol{v}_{c}\right)\right)}{\partial \boldsymbol{v}_{c}} -\frac{\partial \log \left(\exp \left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)\right)}{\partial \boldsymbol{v}_{c}}\\ &=\sum^V_w \boldsymbol{u}_w \hat{y}_w -\boldsymbol{u}_{o}\\ &=\boldsymbol{U}^{T}(\hat{\boldsymbol{y}}-\boldsymbol{y}) \end{aligned}$

对上下文词向量 $\boldsymbol{u}_w$ 求导：

$\begin{aligned} &\frac{\partial J_{\text {naive-softmax}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{w}} \\ &=\frac{\partial \log \left(\sum_{w=1}^{V} \exp \left(\boldsymbol{u}_{w}^{T} \boldsymbol{v}_{c}\right)\right)}{\partial \boldsymbol{u}_{w}}-\frac{\partial \log \left(\exp \left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)\right)}{\partial \boldsymbol{u}_{w}} \end{aligned}$

这个时候就要分情况了，当w=o时：

$\begin{aligned} &\frac{\partial J_{\text {naive}-\text {softmax}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{w}} & \\ &=\frac{\boldsymbol{v}_{c}\exp \left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)}{\sum_{i}^{V} \exp \left(\boldsymbol{u}_{i}^{T} \boldsymbol{v}_{c}\right)} -\boldsymbol{v}_{c}\\ &=(\hat{y}_o-1) \boldsymbol{v}_{c} \end{aligned}$

而当w!=o时：

$\begin{aligned} &\frac{\partial J_{\text {naive}-\text {softmax}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{w}} & \\ &=\frac{\boldsymbol{v}_{c}\exp \left(\boldsymbol{u}_{w}^{T} \boldsymbol{v}_{c}\right)}{\sum_{i}^{V} \exp \left(\boldsymbol{u}_{i}^{T} \boldsymbol{v}_{c}\right)} \\ &=\hat{y}_w \boldsymbol{v}_{c} \end{aligned}$

两种情况可以合并为：

$\begin{aligned} &\frac{\partial J_{\text {naive}-\text {softmax}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{w}} & \\ &=(\hat{y}_w-y_w) \boldsymbol{v}_{c} \\ \\ &y_{w}=\left\{\begin{array}{ll} {1} , {\mathrm{w}=0} \\ {0} , {\mathrm{w} \ne 0} \end{array}\right. \end{aligned}$

从上面的推导结果，我们可以发现一些东西：我们对中心词求导时，只计算了对当前位置c处的中心词的导数，为何呢？因为对其他位置的导数都是0！从J的表达式可以看出，J与除了c其他位置的中心词向量是无关的！而对上下文词求导时，我们发现，无论该词是不是在当前位置o，导数都存在，所以要把词汇表中所有词都计算一遍。

这告诉了我们什么呢？

在参数更新时，更新$V$向量是很容易的，更新$U$向量却很艰难。

# 负采样(Negative Sampling)

上面对朴素softmax损失函数的求导过程中，我们发现了在更新U的时候，计算开销十分大。所以我们要想办法降低这样的计算开销。负采样技术，就是目前在word2vec中最实用的降低计算量的技巧。

假设当前中心词为c，我们从词汇库中选取K个负采样词，记为 $w_1,w_2,...,w_K$ ，其对应的词向量为 $u_1,u_2,...,u_K$ ，要注意选取这些负采样词的时候，要避开当前真实的上下文词o，o实际上是正样本。这样，我们便可以构建一个新的损失函数——负采样损失函数：

$J_{\text {neg-sample }}\left(v_{c}, o, U\right)=-\log \left(\sigma\left(u_{o}^{\top} v_{c}\right)\right)-\sum_{k=1}^{K} \log \left(\sigma\left(-u_{k}^{\top} v_{c}\right)\right)$

这个损失函数，一眼就可以看出比naive-softmax loss求导要更容易，因为，它在更新U矩阵时，只更新了K+1个向量，而naive-softmax需要更新U中的全部向量。而在负采样损失函数中，我们不再使用softmax激活函数了，而是使用sigmoid函数。所以，很多人也会说，负采样是把原本的一个softmax的|V|类分类变成了少数几个二分类问题。

我们对这个损失函数再仿照上一节的方法求个导。

在求导前，我们可以先计算一下sigmoid函数求导的特点，这样可以方便我们求导：

$\frac{\partial \sigma(x)}{\partial x}=\sigma(x)(1-\sigma(x))$

对中心词向量 $\boldsymbol{v}_c$ 求导：

$\begin{align} &\frac{\partial J_{n e g-\text {sample}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{v}_{c}} \nonumber \\ &=-\left(1-\sigma\left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)\right) \boldsymbol{u}_{o}+\sum_{k=1}^{K}\left(1-\sigma\left(-\boldsymbol{u}_{k}^{T} \boldsymbol{v}_{c}\right)\right) \boldsymbol{u}_{k} \nonumber \end{align}$

对上下文词向量 $\boldsymbol{u}_o$ 求导：

$\begin{align} &\frac{\partial J_{neg-sample}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{k}} \nonumber \\ &=-\left(1-\sigma\left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)\right) \boldsymbol{v}_{c} \nonumber \end{align}$

对上下文词向量 $\boldsymbol{u}_k$ 求导：

$\begin{align} &\frac{\partial J_{neg-sample}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{u}_{k}} \nonumber \\ &=\left(1-\sigma\left(-\boldsymbol{u}_{k}^{T} \boldsymbol{v}_{c}\right)\right) \boldsymbol{v}_{c} \nonumber \end{align}$

# window loss

上面写的损失函数，都是针对单个词对<c,o>的损失，而skip-gram采用的是滑动窗口机制，所以我们需要进一步计算一整个上下文窗口（context window）中的损失：

$J_{\text {skip-gram }}\left(v_{c}, w_{t-m}, \ldots w_{t+m}, U\right)=\sum_{-m \leq j \leq m} J\left(v_{c}, w_{t+j}, U\right)$

等式后面的那个J可以替换成naive-softmax loss或者negative sampling loss，这里不再赘述。

# Word2Vec的编程实现

这个就是cs224n作业2的编程部分了。

当然，我们肯定不是从零到一实现一个word2vec算法，这还是太复杂了，作业主要是填空的形式，让我们把算法的核心部分给填写了一下。至于很多系统的设计我们是不同操心的。

我们需要编写的，主要是这么四部分：
A. naive softmax loss及其求导结果
B. negative sampling loss及其求导结果
C. 一个window的loss的计算
D. SGD优化算法中的参数更新

其实这些部分，就是根据我们上面计算的各种求导结果来写，而且我们的求导结果已经是矩阵运算了，十分方便。我写的代码已经上传到github上：
https://github.com/beyondguo/CS224n-notes-and-codes/tree/master/assignment2

我这里想单独记录一下一些编程技巧：

numpy中各种矩阵运算的维度问题
如何用Vectorization来替换掉低效的for训练。

# python乘法、np.multiply()和np.dot()

一图以蔽之：

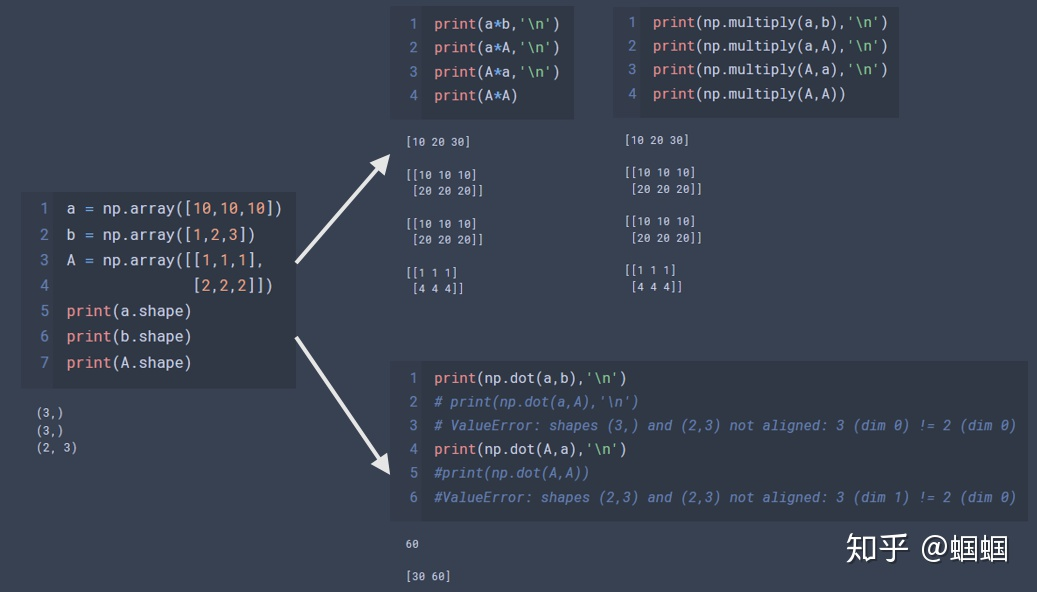
总之，np.multiply()和普通的乘法没有区别，在形状相同的情况下，它们都是“对应元素相乘”，保留原形状。当形状不一的时候，小矩阵会利用“传播机制”，乘到大矩阵上。

而np.dot则是正经的矩阵相乘，需要符合维数的限制，维度不对就会报错。唯一的特例就是两个向量进行点积，这个时候不用使用转置。

# 关于Vectorization

np中所有的函数都可以作用于标量、向量、矩阵，因此，如果需要对一个矩阵中所有的元素采取相同的函数动作，那可以直接把整个句子丢进np函数中。另外，我们在进行计算的时候，如果最后要求的对象是矩阵，那最好在推导的时候，就写成矩阵的形式，这样避免了很多不必要的for循环。

例如，在作业中，我们需要求一个J对U的导数，在求导时，我们前面已经计算好了：

那J对U的导数，就是把U的每一列的导数求出来，再拼起来。但是，其实我们可以直接把这个过程写成矩阵的形式：

$\begin{aligned} &\frac{\partial J_{\text {naive}-\text {softmax}}\left(\boldsymbol{v}_{c}, o, \boldsymbol{U}\right)}{\partial \boldsymbol{U}} & \\ &=\boldsymbol{v}_{c}(\hat{y}-y)^T \end{aligned}$

下面两张图展示了我们的变换过程：

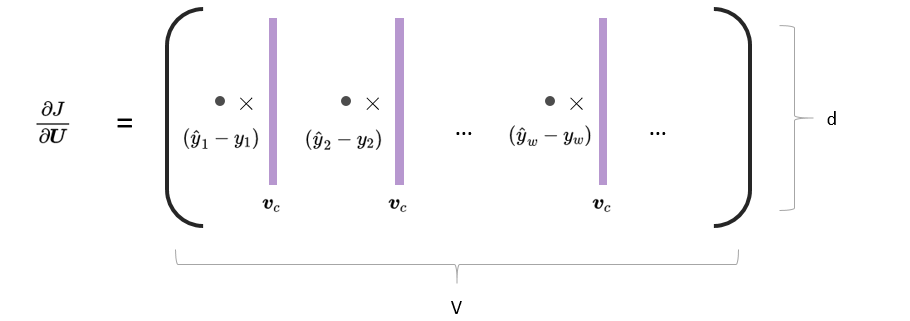
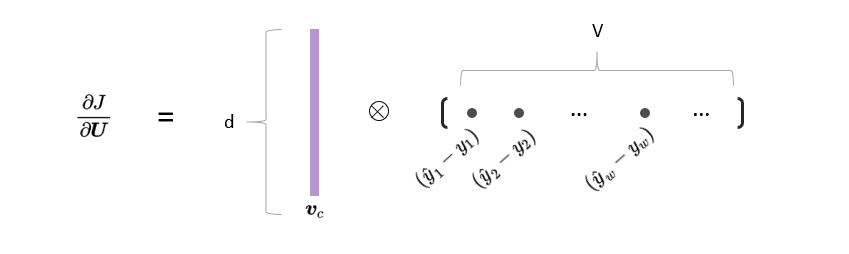
因此，如果按照for循环的方式，代码就是分别对U的每一个向量 $u_w$ 求导之后再拼成一个矩阵：

gradU = np.array([v_c*(softmax(np.dot(U.T,v_c))[x]-int(x==o)) \
for x in range(U.shape[0])])

1
2

而如果使用我们前面算出来的矩阵的表示形式，那代码就是这样：

gradOutsideVecs = np.dot((y_hat-y).reshape(-1,1),v_c.reshape(1,-1))  
# (V,),(d,)-->(V,d)

1
2

后者的执行效率会高很多。

# numpy其他的一些有趣有用的功能

这里列举两个我觉得很使用的功能吧：

通过一个array直接取出ndarray对象中一系列指定序号的元素

下面的两个例子：

a = np.array([0,10,20,30,40,50,60,70])
indices = np.array([0,2,4,6])
a[indices]

1
2
3

输出：array([ 0, 20, 40, 60])

A = np.array([[1,1,1],
              [2,2,2],
              [3,3,3]])
indices = np.array([0,2])
A[indices]

1
2
3
4
5

输出： array([[1, 1, 1],[3, 3, 3]])

无论是数组还是矩阵，都可以直接取。需要注意的是，这里的indices必须是np.array的格式。

通过at函数往指定位置进行运算

比如我们有一个大矩阵，我们希望向其中的某一些列中加上一堆值。例如：

C = np.zeros((5,3))
temp = np.ones((2,3))
print('C:\n',C)
print('temp:\n',temp)

1
2
3
4

看一看C和temp是什么：

C:
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
temp:
 [[1. 1. 1.]
 [1. 1. 1.]]

1
2
3
4
5
6
7
8
9

接下来，我们想temp中的两个向量的值，加到C中的第0行，第2行，我们只用写：

np.add.at(C,[0,2],temp)
C

1
2

输出：

array([[1., 1., 1.],
       [0., 0., 0.],
       [1., 1., 1.],
       [0., 0., 0.],
       [0., 0., 0.]])

1
2
3
4
5

看！就是这么方便！其中，add可以替换成其他各种运算。

以上。