# 「杂谈」神经网络中的激活(Activation)函数及其对比
神经网络的每一层基本都是在一个线性运算后面来一个非线性激活函数(Activation function),再把值传给下一层的。激活函数有多种,这篇文章主要就是介绍各种激活函数和它们的对比。
# 为啥要有非线性的激活函数(non-linear activation function)
什么是线性函数?就是形如y=ax+b这样的函数。我们知道,n和线性函数嵌套起来,还是线性函数: y=a1(a2x+b2)+b1 =a1a2x+a1b2+b1 =cx+d 而我们每一层的输入,都是按照Z=WX+b这样的线性公式在计算的,再经过一个线性的激活,还是线性的。然后经过下一层,还是线性的,也就是中间不管多少层,最后的结果,依然是最初的输入X的线性表示,那不就相当于只有一层了吗? 这样,n层的神经网络,就相当于一个简单的Logistic regression了。
因此,我们必须采用一个非线性的激活函数,让每一层都有意义,让每一层都有其特定的功能!
下面逐一介绍各种非线性激活函数:
# 一、sigmoid函数(σ)
这玩意儿大家最熟悉了,放个图:
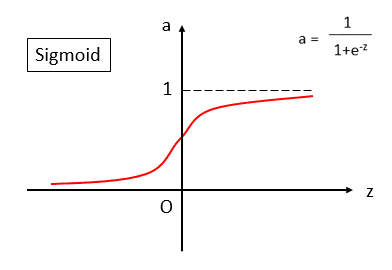
图画的还可以吧,纯PPT画图...( ・´ω`・ )
这个也没什么好讲的了,公式图上也给出了。 它的求导可以稍微记忆一下: a(z)' = a(z)×[1-a(z)] 毕竟如果我们需要自己推导梯度下降的过程的话,这个求导公式还是很有用的。
sigmoid的特点如下:
- 很好的拟合了0,1输出,常作为二分类问题(binary classification)的激活函数。
- 它的导数为两边小中间大。
# 二、tanh函数
这个又叫“双曲正切”函数,也是直接上图:
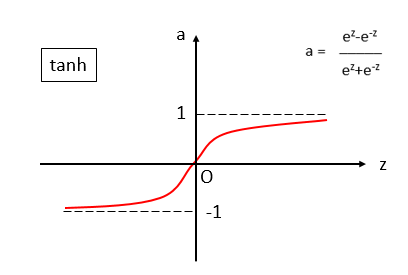
有人会说:诶?跟sigmoid长的好像哟~ 对了!它就是sigmoid向下平移了一个单位得到的。形状是一模一样的。 它的导数也很有特点: a(z)' = 1-[a(z)]2
相比于sigmoid,它的关于原点对称的,根据吴恩达的说法,这样的性质使得模型在训练时性能往往比sigmoid更好,因此在中间层一般都不用sigmoid作为激活函数,而用tanh来代替。但是在output层,对于二分类问题,我们都要使用sigmoid,因为要拟合0,1的输出。
# ——sigmoid和tanh共同的问题:
当z比较大或者比较小的时候(也就是在曲线的两头),函数的导数会非常小,会导致参数的梯度也非常小,这样我们在用梯度下降法进行训练的时候就会非常慢,尤其是当数据量很大的时候。
因此,我们有了下面的函数:
# 三、ReLU函数
ReLU的全称是Rectified linear unit(线性整流单元)。听起来好像很复杂的样子,其实就是一个贼简单的分段函数,小学生都会画的:
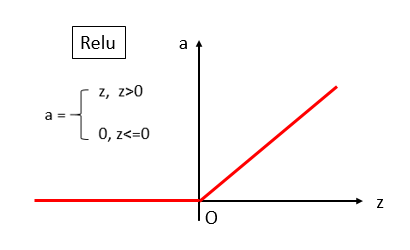
其实,它的公式可以用一行来表示:a=max(z,0),在python中就是一行代码。
有时是真是忍不住说它是线性函数,毕竟每一段都是线性的,但是人家就是实实在在的非线性函数,它不会使多层神经网络退化成单层。 但是因为它每一段都是线性的,而且导数要么是0,要么是1,计算简单,大小合适,因此梯度下降算起来很快,于是迅速被广泛地使用了起来,完美地替代了sigmoid、tanh这些激活函数。(只是多数情况,有一些特殊的网络还是会使用tanh和sigmoid,比如RNNs)
ReLU看起来有点简单粗暴了,有人觉得导数为0的那一段看的不顺眼,于是发明了Leaky ReLU,顾名思义,就是把那一段也掰下来一点:
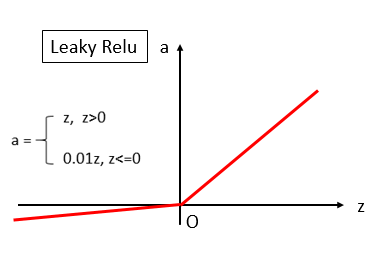
据说效果可以比ReLU更好一些。
ReLU还有很多其他的变体,但是最最常使用的效果最稳定的还是ReLU。 因此,之后在设计神经网络的时候,选择激活函数我们就可以放心大胆地选择ReLU,它不仅速度快,而且效果好。
其实我最开始也有疑问,ReLU按道理比sigmoid简单多了,为什么反而效果更好?一般情况下,不是越简单的效果越不好吗? 其实深度学习中,模型不是最重要的,尤其是在业界,大家广泛使用的也许并不是最先进最复杂的模型,而是一个经典的简单的模型。比模型更重要的是数据。有足够多的训练样本,迭代足够多的次数,简单的模型也可以达到极好的效果。ReLU的优势就在于其简单迅速,因此在短时间内可以进行大量的迭代,因此在业界得到广泛的使用。
# 2018.8.10更新:
今天突然发现之前漏了一个重要的激活函数:Softmax
# 四、Softmax
Softmax可以看做是对sigmoid的一种推广。我们在做二分类问题的时候,一般都使用sigmoid作为输出层激活函数,因为它的范围在0~1之间。但是如果我们需要进行多分类呢? 于是我们有了Softmax函数。
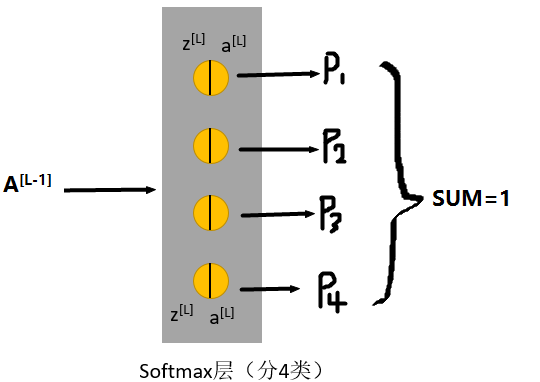
Z的计算跟所有其他激活函数一样,都是线性运算:Z=WA[l-1]+b 然后A怎么计算呢: a = ez/sum(ez) a就相当于图上的[p1,p2,p3,p4]组成的向量。 其中各个分量之和为1,这从公式也可以很容易看出来。这样,每一个分量就代表该类别的概率。
对于多分类问题,我们采用的损失函数也稍有不同: L(y,y^) = -Σyi·logy^i 也称为交叉熵(crossentropy)。
好了,关于这个激活函数的内容差不多就这些了。
