从直觉上理解什么是最速下降法&共轭梯度法

本文仅用于记录一下有关最速下降法和共轭梯度法的一些不容易理解的地方，不做很深入的探究，因为我也不做优化方向。更多的是希望让自己从直觉/逻辑上去理解这两种算法。

首先讲讲我们的问题背景： 求解大规模线性方程Ax=b，如果直接求解，就涉及到求A的逆，这对于大型矩阵来说很困难。Ax=b可以转化为一个二次优化问题：$min\ f(x) = 1/2 x^TAx -bx$，令f(x)导数为0就等价于Ax=b。对于二次优化问题，我们可以使用基于梯度的方法来迭代求解。其中的两个代表算法是“最速下降法”和“共轭梯度法”。当然还有很多其他算法，我们不在这里讨论。

最速下降法（Steepest Descent）

最速下降法我的理解它是梯度下降法的一种特殊方式，梯度下降法我们需要事先设置步长，而最速下降法是通过每步都求解一个优化问题来确定最优的步长是多大，所以每一步都是走到当前方向上最低点。这也是最速下降法的思想。 关于最速下降法，我们可以通过下面几个等高线图加深理解：

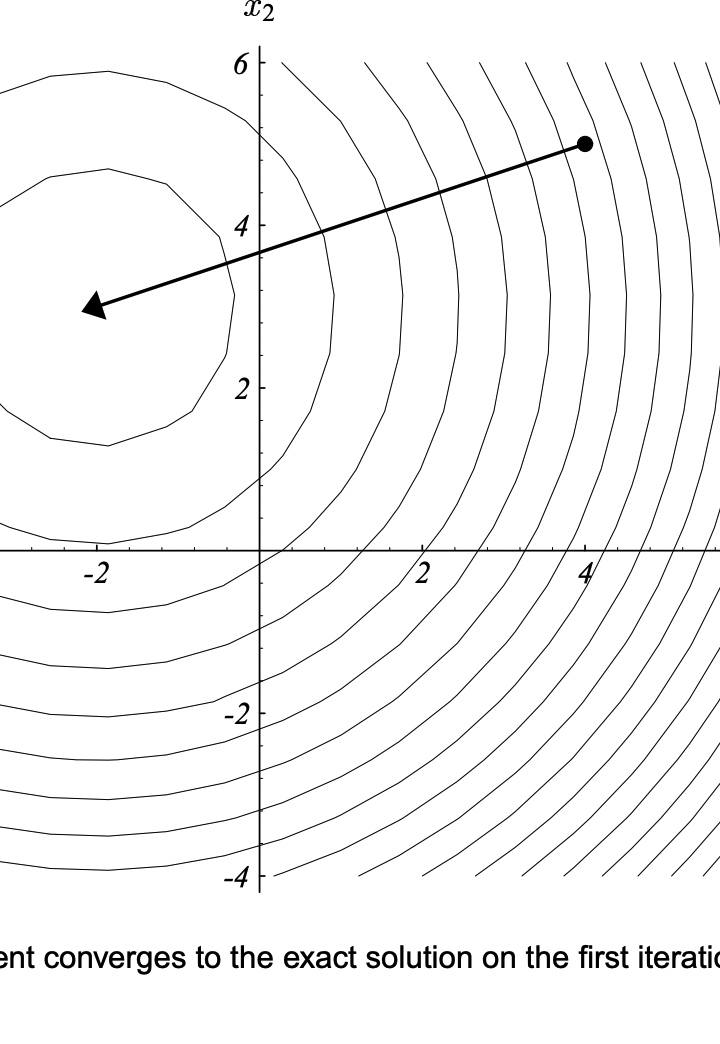
这个图说的是，如果你的优化问题就很对称的，也就是特征值都相同，就好比在你吃饭的碗🥣里做优化，那使用最速下降法其实可以一步到位。因为任何一个初始点的梯度的反方向都指向最低点，然后再这个方向上做一个“线搜索”，就可以确定最优解。 但是，多数的优化问题不是这样规规矩矩的，多半都是歪的/扁的/瘪的。比方对于一个二次优化，两个维度上的特征值不一样。那么使用最速下降法的话，收敛速度就很受初始点的影响：

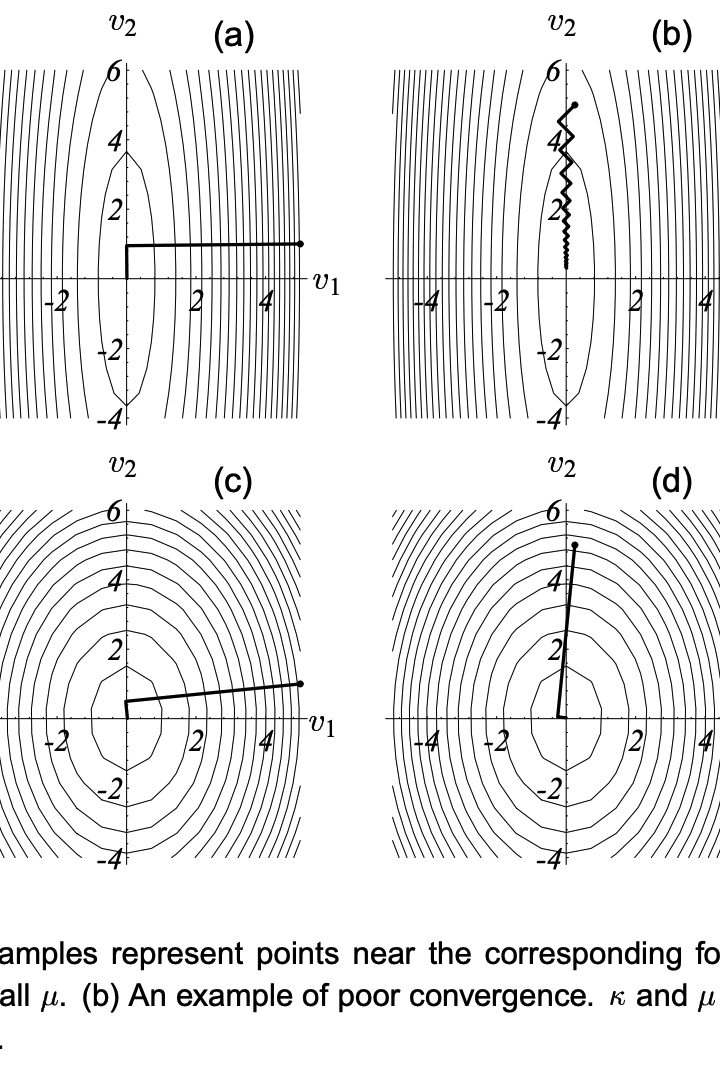
图中，等高线曲线越扁，这个优化问题的“条件数”就越大。我们可以发现，当条件数小的时候，收敛速度会比较快（见图中的c，d），这个时候初始点的影响不是很大。但是当条件数大的时候，如果初始点选的好，比方正好选在了一个梯度方向会下降非常快的方向，那么也可以很快接近最低点（如图中a）。但如果初始点的梯度方向是一个不那么好的方向，那么就会反复碰壁（如图中b），收敛会非常慢。 然后就是最速下降法的每一步都会跟上一步正交。这一点也很有趣。

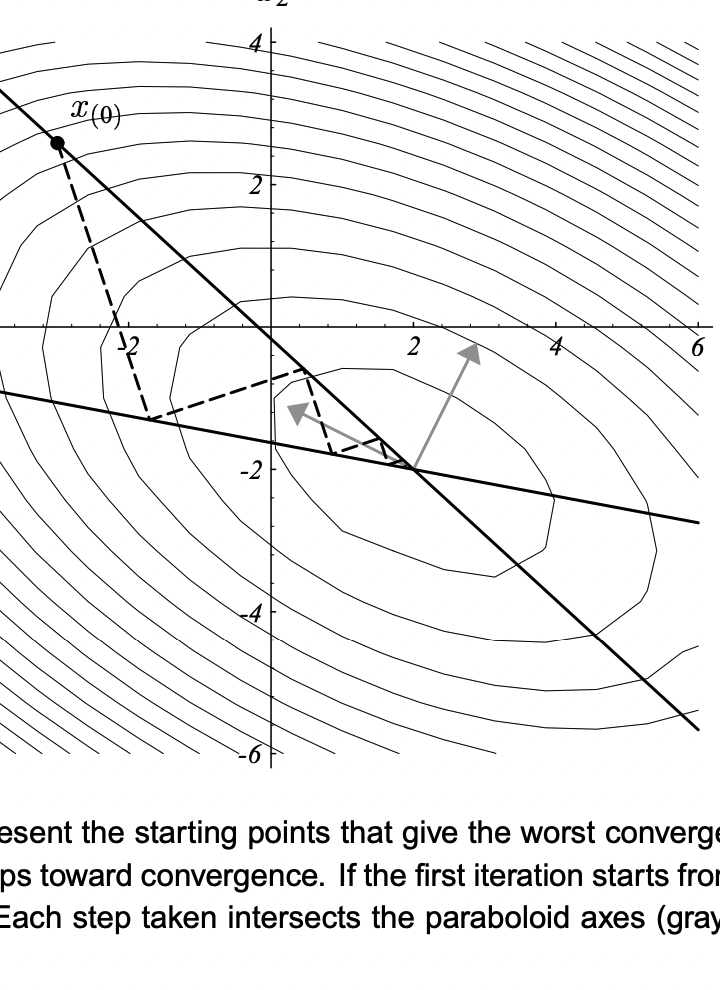
关于这个特点，首先我们从直觉上去理解： 如果当前步的方向不跟上一步方向正交，那说明当前的方向还有上一步方向的分量，那说明上一步并没有达到最优。所以，只要上一步是那个方向上的最低点，那我这一步就不能有上一步方向上的任何分量，那就只能跟它正交了。 推导的话也简单： 我们设损失函数为f(x)，初始点为$x_0$，那么该点处的梯度就是 $f^{'}(x_0)$，计作$\nabla f(x_0)$。下一个点是$x_1=x_0 - \alpha \nabla f(x_0)$，我们需要通过线搜索来寻找最优的\alpha使得它在这个方向上最小：

$$min\ \ f(x_0 - \alpha \nabla f(x_0)) \\$$

求解这个问题，就是让这个函数对\alpha的倒数为0，即：

$$\begin{align} \frac{\partial f(x_0 - \alpha \nabla f(x_0))}{\partial \alpha} &= f^{'}(x_0 - \alpha \nabla f(x_0))(-\nabla f(x_0)) \\ &=-\nabla f(x_1)\nabla f(x_0)= 0 \\ \end{align} \\$$

所以，相邻两步的梯度方向是正交的。

共轭梯度法（Conjugate Gradient）

最速下降法，本来从名字来看，已经够牛逼了，已经最速了，还能怎么样？可惜啊，这里的最速，是“只顾眼前”的最速，只是在当前梯度方向最速了，但是通过上面的一些图我们可以看到，同一个方向，可能会在后面不断重复地走，也就呈现出所谓的“锯齿状”的路径，这样的优化路径其实很低效，最差的情况下到达最低点可能需要无限步（见第三张图）。

共轭梯度法，我们先不管这个“共轭”是啥意思，它主要想解决的就是这样的一个问题，就是能不能“不走老路”？它的想法比最速下降法更加大胆：我不管是当前这一步不走老路（最速下降法的思想），我还希望我的每一步，都不走老路！ （这里所谓的“路”，就是方向的意思）

这可牛逼了，如果这样的想法可以实现的话，那么，对于一个k维的凸优化问题，我最多只需要k步就可以到达最优点。

为了理解“共轭”这个奇怪的概念，我也看了好多相关的讲解，但总感觉逻辑怪怪的，一直没法从直觉上得到一个很好的理解。但是量变引起质变，看了好多篇讲解之后，我突然悟了，从下面一个小例子来理解：

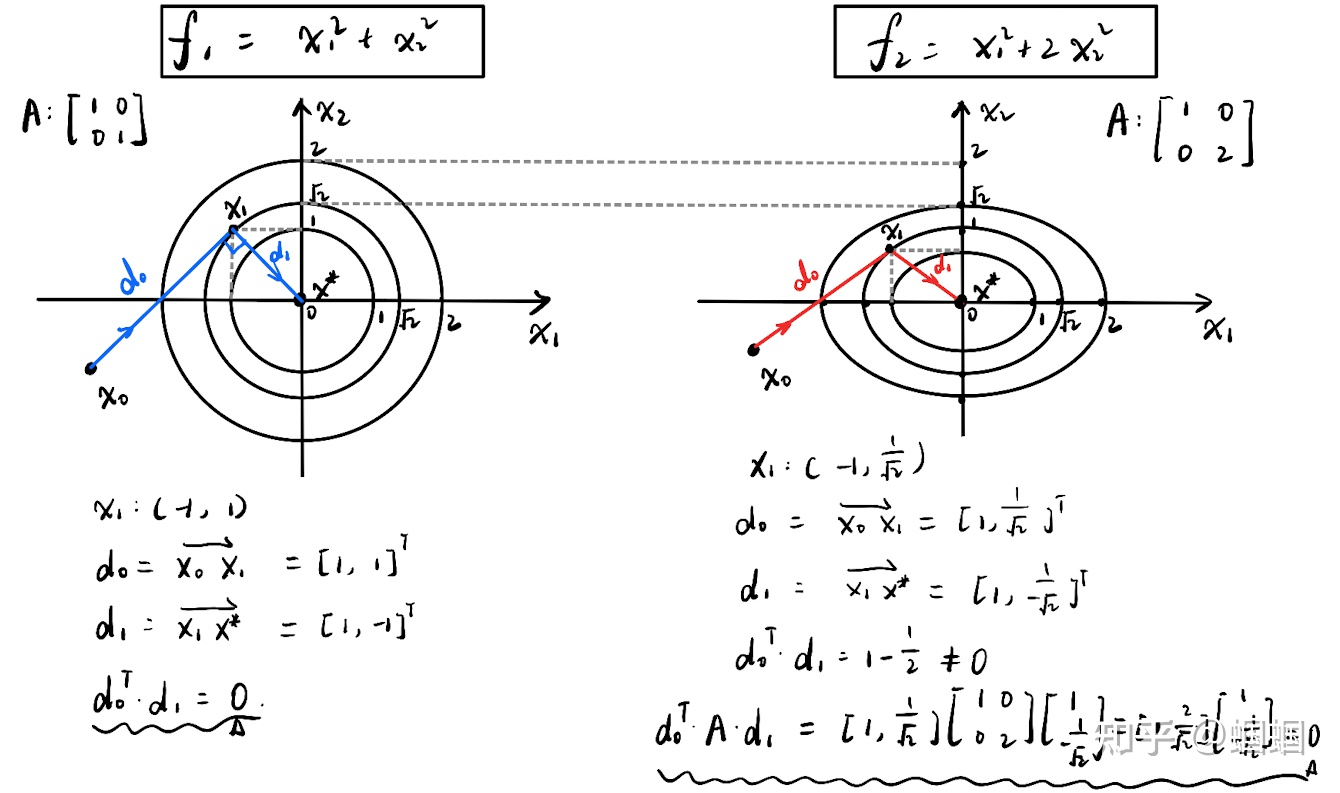
左边的图展示了一个系数矩阵的特征值都相等的二次优化问题。任意一个初始点(x0)，任意一个方向(d0)，总能跟某一条等高线相切，切点就是沿着该方向的最低点（x1）了。该点的切线方向（d1）肯定跟d0垂直（前面证明过），并且沿着这个方向，肯定可以达到极值点（x*）。这也就是前面讲的，只要A很规则/等高线很规则，那么我通过两步，就一定可以找到极值点。这个道理很好理解吧。

现在的情况变了，我们的等高线被压扁了，见右图，其实就是x2轴的方向压缩了一下（体现在A上就是特征值不相等了），图上的所有元素都要压缩，原来的蓝色的优化路径，现在被压缩成了图中红色的路径。

这个时候显而易见，d0和d1已经不垂直了，即$\mathbf{d_0^Td_1\not= 0}$。但是，我们发现：$\mathbf{d_0^TA d_1= 0}$。

也就是说，被压缩之后，最佳的优化路径还是存在着某种特殊的固定的联系。对于规则的等高线，最优路径之间是正交的，而对于不规则的等高线，最优路径之间是“关于A正交”的。这个“关于A正交”，就是所谓的“共轭”关系！ 我觉得这样理解就很容易懂了。也就是说，两个向量关于A共轭，那么这两个向量在原始的某个映射中应该是正交的。这里再借用下图来辅助说明一下：

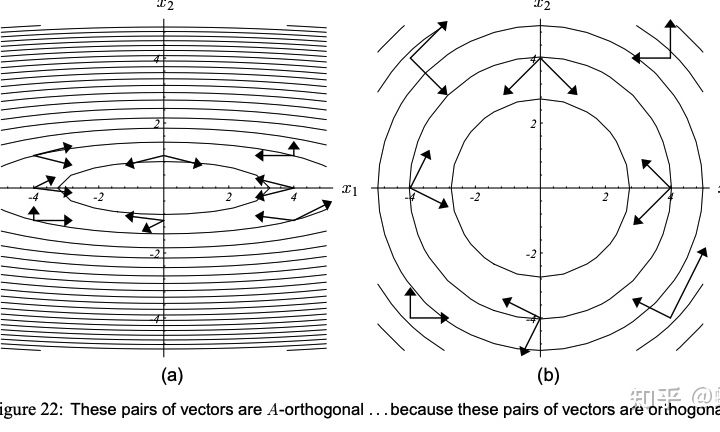
上图的意思是：当两个向量共轭，那么把他们所在的等高线曲面拉成一个规规矩矩的圆形的话，就会变成正交。

总之：以求解线性方程（转化为二次优化），第一步怎么走大家都知道：任何一个初始点，先计算梯度，然后进行线搜索找到当前方向的最低点。关键是下一步往哪个方向走，如果沿着正交的方向，那么运气不好就会反复在等高线内壁弹来弹去，而如果使用与上一步共轭的方向，那就可以直达最优点。

知道了什么是共轭，共轭梯度法就很好理解了。

共轭梯度法，就是对于k维的一个问题，找出k个互相共轭的方向，然后每一步都沿着这个方向走到极致。当k步走完，优化问题就求解了。

至于怎么找出这k个互相共轭的方向，前面我们提到了系数矩阵的特征值，其实我们可以通过特征分解来推导出来，但这样的计算量依然很大。这里有现成的计算量小的办法来求解，具体怎么推导出来的我就不想细究了（真的不太关心），根据《花书》，对于 $\boldsymbol{d}_{t}=\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})+\beta_{t} \boldsymbol{d}_{t-1}$，我们可以通过下面的两种方法来迭代地求解每一步的方向：

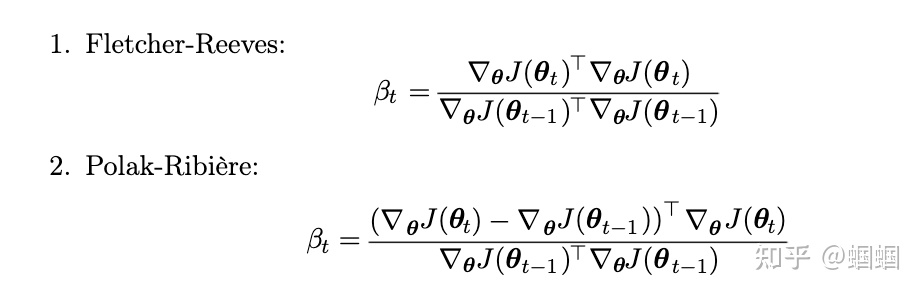
共轭梯度法，是一种一阶优化算法，比最速下降法高效，又没有牛顿法那样计算复杂，因此是最常用的大规模线性规划的算法之一。

---

本文参考的主要资料：

• 《Deep Learning》，即“花书”；
• 《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》 （http://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf ） 这个强烈推荐，虽然我只是粗略了读了几页，但感觉是我看过的最富直觉的讲解之一了；
• 共轭梯度法（一）：线性共轭梯度 - 王金戈的文章 - 知乎 （https://zhuanlan.zhihu.com/p/98642663）这个我也强烈推荐，作者也是由浅入深，娓娓道来（虽然我也没完全看懂，不过纯属是我太菜）。